Cho hình vuông ABCD có cạnh 1 dm. Tính cạnh của tam giác đều AEF có E thuộc CD, F thuộc BC

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng 1dm . Tính cạnh của tam giác đều AEF có E thuộc CD , F thuộc BC.
Đặt DE = x thì CE = 1 - x thì CF = CE = 1 - x , AE 2 = x2 + 1
Từ CE2 + CF2 = EF2 , ta có 2 ( 1 - x ) 2 = x2 + 1.
Đưa về phương trình
x2 - 4x + 4 = 3 <=> (x-2)2 = 3 <=> x = 2 +- \(\sqrt{3}\)
Do x < 1 nên ta chọn x = 2 -\(\sqrt{3}\)
EF = ( 1 - x ) \(\sqrt{2}\)= (\(\sqrt{3}\)- 1 )\(\sqrt{2}\) = \(\sqrt{6}\)- \(\sqrt{2}\)(dm)
Đúng 0
Bình luận (0)
Có: \(\Delta ADE=\Delta ABF=CF=CE\)
Lại có: \(\hept{\begin{cases}2CF^2=EF^2\\\left(1-CF\right)^1+1=EF^2\end{cases}}\)
\(\Rightarrow EF\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 1 dm. Tính cạnh hình tam giác đều AEF có E thuộc CD. F thuộc BC
Cảm ơn mọi người !
Cho hình vuông ABCD cạnh 1dm. Tính cạnh tam giác đều AEF ( E thuộc CD, F thuộc BC)
Đáp án trong NCPT có r nhưng mk thắc mắc tại sao CE=CF
Giúp nhé
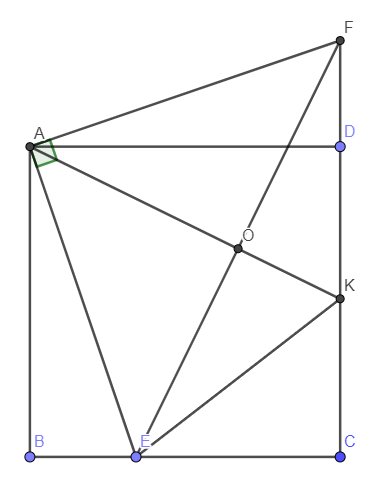
Cho hình vuông ABCD và điểm E tùy ý trên cạnh BC. Tia Ax vuông góc với AE tại A cắt CD kéo dài tại F. Kẻ trung tuyên AI của tam giác AEF và kéo dài cắt cạnh CD tại K.a, Chứng minh AE AFb, Chứng minh các tam giác AKF, CAF đồng dạng và
A
F
2
K
F
.
C
F
c, Cho AB 4 cm, BE ...
Đọc tiếp
Cho hình vuông ABCD và điểm E tùy ý trên cạnh BC. Tia Ax vuông góc với AE tại A cắt CD kéo dài tại F. Kẻ trung tuyên AI của tam giác AEF và kéo dài cắt cạnh CD tại K.
a, Chứng minh AE = AF
b, Chứng minh các tam giác AKF, CAF đồng dạng và A F 2 = K F . C F
c, Cho AB = 4 cm, BE = 3 4 BC. Tính diện tích tam giác AEF
d, Khi E di động trên cạnh BC, tia AE cắt CD tại J. Chứng minh biểu thức A E . A J F J có giá trị không phụ thuộc vị trí của E

a, Ta có ∆ABE = ∆ADF(g.c.g) => AE = AF
b, Ta có: ∆AKF ~ ∆CAF ( F ^ chung và F A K ^ = F C A ^ = 45 0 )
=> A F H F = C F A F => A F 2 = K F . C F
c, S A E F = 93 2 c m 2
d, Ta có: AE.AJ=AF.AJ=AD.FJ
=> A E . A J F J = AD không đổi
Đúng 0
Bình luận (0)
cho hình vuông ABCD,E thuộc BC qua A kẻ tia Ax vuông góc AE cắt CD tại F.trung tuyết Ay của tam giác AEF cắt CD ở K
a,chứng minh rằng AF2 = FK.FC
b,chứng minh rằng khi E di chuyển trên cạnh BC thì chu vi tam giác EKC có giá trị không đổi
Cho hình vuông ABCD có cạnh 1dm. Tính cạnh của tam giác đều AEF có E thuộc CD, F thuộc BC.
cho hình vuông ABCD,E thuộc BC qua A kẻ tia Ax vuông góc AE cắt CD tại F.trung tuyết Ay của tam giác AEF cắt CD ở K a,chứng minh rằng AF^2 = FK . FC b,chứng minh rằng khi E di chuyển trên cạnh BC thì chu vi tam giác EKC có giá trị không đổi
cho hình vuông ABCD,E thuộc BC qua A kẻ tia Ax vuông góc AE cắt CD tại F.trung tuyết Ay của tam giác AEF cắt CD ở K a,chứng minh rằng AF^2 = FK . FC b,chứng minh rằng khi E di chuyển trên cạnh BC thì chu vi tam giác EKC có giá trị không đổi
Cho hình vuông ABCD điểm E thuộc cạnh CD điểm F thuộc cạnh BC sao cho chứ vi tam giác CFE bằng nửa hình vuông ABCD . Chứng minh rằng góc FAE bằng 45°