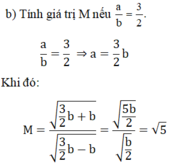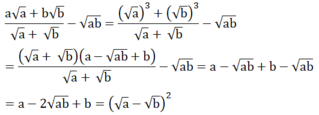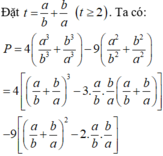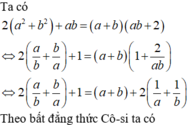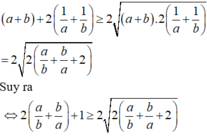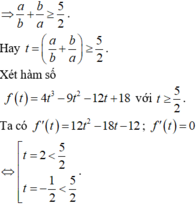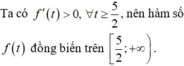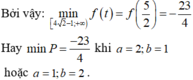CM:a2+b2-ab-a+b+2>0

Những câu hỏi liên quan
với ab khác 0 cm:a2/b2+b2/a2>=2(a/b+b/a)
Đề bài ko đúng bạn.
Với \(a=b=1\) thay vào \(\Rightarrow1+1\ge2\left(1+1\right)\Rightarrow2\ge4\) (sai)
B1:Cho a>0, a2=bc
a+b+c=abc
Cmr:
a lớn hơn hoặc bằng căn3,b>0,c>0,b2+c2 lớn hơn hoặc bằng 2a2
B2: Cho hệ
a2+b2+c2=2
ab+bc+ca=1
Cmr: a,b,c thuộc {-4/3;4/3}
B2: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)=4\)
\(\Rightarrow\orbr{\begin{cases}a+b+c=2\\a+b+c=-2\end{cases}}\)
TH1: \(a+b+c=2\Rightarrow c=2-\left(a+b\right)\)
\(a^2+b^2+c^2=2\)\(\Leftrightarrow a^2+b^2+\left(2-a-b\right)^2=2\)
\(\Leftrightarrow a^2+b^2+ab-2\left(a+b\right)+1=0\)
\(\Leftrightarrow a^2+\left(b-2\right)a+b^2-2b+1=0\)
Xem đây là một phương trình bậc hai ẩn a, tham số b.
Để tồn tại a thỏa phương trình trên thì \(\Delta\ge0\)
\(\Leftrightarrow\left(b-2\right)^2-4\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow b\left(3b-4\right)\le0\)\(\Leftrightarrow0\le b\le\frac{4}{3}\)
Do vai trò của a, b, c là như nhau nên \(0\le a,b,c\le\frac{4}{3}\)
(hoặc đổi biến thành b và tham số a --> CM được a, rồi thay \(b=2-c-a\) sẽ chứng minh được c)
TH2: \(a+b+c=-2\) --> tương tự trường hợp 1 nhưng kết quả sẽ là
\(-\frac{4}{3}\le a,b,c\le0\)
Kết hợp 2 trường hợp lại, ta có đpcm.
Đúng 0
Bình luận (0)
Cho a,b>0 và a+b=1. Tìm Min F=2/ab + 1/(a2+b2) + (a4+b4)/2
Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: a 2 < ab và ab < b 2
Với a > 0, b > 0 ta có:
a < b ⇒ a.a < a.b ⇒ a 2 < ab (1)
a < b ⇒ a.b < b.b ⇒ ab < b 2 (2)
Đúng 0
Bình luận (0)
Cho a,b,c>0. CMR: 3(a2+b2+c2)≥(a+b+c)2≥3(ab+bc+ca)
Cho biểu thức:
M
a
a
2
-
b
2
+
1
+
a
a
2
-
b
2
:
b
a
-...
Đọc tiếp
Cho biểu thức:
M = a a 2 - b 2 + 1 + a a 2 - b 2 : b a - a 2 - b 2 với a > b > 0
b) Tính giá trị M nếu a b = 3 2
a,b,c≥0
a2+b2+c2=6
cmr: 5ac−15≤2(ab+bc+abc)≤7+5ac
Đặt \(P=2ab+2bc+2abc-5ac\), ta sẽ chứng minh \(-15\le P\le7\)
Ta có:
\(P=2b\left(a+c\right)+2abc-5ac\le b^2+\left(a+c\right)^2+2abc-5ac\)
\(P\le a^2+b^2+c^2+2abc-3ac=6+2abc-3ac=ac\left(2b-3\right)+6\)
- Nếu \(b\le\dfrac{3}{2}\Rightarrow P< 6< 7\) (đúng)
- Nếu \(b>\dfrac{3}{2}\Rightarrow P\le\dfrac{1}{2}\left(a^2+c^2\right)\left(2b-3\right)+6=\dfrac{1}{2}\left(6-b^2\right)\left(2b-3\right)+6\)
\(\Rightarrow P\le7-\dfrac{1}{2}\left(b-2\right)^2\left(2b+5\right)\le7\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(1;2;1\right)\)
Đồng thời:
\(P=2\left(ab+bc+abc\right)-5ac\ge-5ac\ge-\dfrac{5}{2}\left(a^2+c^2\right)=-\dfrac{5}{2}\left(6-b^2\right)=-15+\dfrac{5}{2}b^2\ge-15\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\sqrt{3};0;\sqrt{3}\right)\)
Đúng 1
Bình luận (0)
Chứng minh đẳng thức:
a
a
+
b
b
a
+
b
-
a
b
a
-
b
2
v...
Đọc tiếp
Chứng minh đẳng thức: a a + b b a + b - a b = a - b 2 v ớ i a > 0 , b > 0
Cho
a
.
b
∈
ℝ
;
a
,
b
0
; thỏa mãn
2
(
a
2
+
b
2
)
+
a
b
(...
Đọc tiếp
Cho a . b ∈ ℝ ; a , b > 0 ; thỏa mãn 2 ( a 2 + b 2 ) + a b = ( a + b ) ( a b + 2 ) . Giá trị nhỏ nhất của biểu thức P = 4 ( a 3 b 3 + b 3 a 3 ) - 9 ( a 2 b 2 + b 2 a 2 ) bằng
A. - 10
B. - 21 4
C. - 23 4
D. 23 4
B1:Cho a>0, a2=bc a+b+c=abc
Cmr: a lớn hơn hoặc bằng căn 3,b>0,c>0,b2+c2 lớn hơn hoặc bằng 2a2
B2: Cho hệ
a2+b2+c2=2
ab+bc+ca=1
Cmr: a,b,c thuộc {-4/3;4/3}
Trả lời giúp mk với .. tối mk học lẹ rồi
Thanks các bạn nhiều