Cho tam giác ABC và điểm O nằm bên trong tam giác đó .M;N;P lần lượt là trung điểm của BC;CA;AB.Trên các tia OM;ON;OP lấy các điểm A';B';C' sao cho M;N;P lần lượt là trung điểm của OA' ;OB';OC'. CM:tam giác ABC=tam giác A'B'C'

Những câu hỏi liên quan
Cho tam giác ABC. Điểm O nằm bên trong tam giác.
Biết các tam giác AOC, AOB, BOC có diện tích bằng nhau.
AO cắt BC tại M.
Khi đó AO/OM
Cho tam giác ABC cân tại A và M là một điểm nằm bên trong tam giác đó sao cho góc AMB lớn hơn góc AMC . Chứng minh MB < MC
Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Đúng 0
Bình luận (0)
Cho điểm O nằm trong tam giác ABC . Gọi M,N,P lần lượt là trung điểm của OA,OB,OC. Khi đó tỉ ố diện tích của tam giác MNP và tam giác ABC bằng
Cho tam giác ABC nhọn nội tiếp đường tròn ( O,R ). Gọi M và I là trung điểm của BC và AC. Giả sử O nằm trong tam giác AMC hoặc O nằm giữa A và M .
a) Chu vi tam giác MIC > 2R
b) Chu vi tam giác ABC > 4R
mở pdf sách nâng cao và phát triển toán 9 tập 1 trang 221
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác đó (O không nằm trên các cạnh tam giác). Điểm M nằm trên tia OA (M khác O,A) sao cho đường tròn ngoại tiếp tam giác ABM cắt tia OB tại giao điểm thứ 2 là N; đường tròn ngoại tiếp tam giác ACM cắt tia OC tại giao điểm thứ 2 là P. Gọi I,J lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, MNP. Lấy E đối xứng với N qua OI. CMR: M,E,P,N cùng thuộc một đường tròn.Giúp mình với! Cảm ơn!
Đọc tiếp
Cho tam giác ABC và điểm O nằm trong tam giác đó (O không nằm trên các cạnh tam giác). Điểm M nằm trên tia OA (M khác O,A) sao cho đường tròn ngoại tiếp tam giác ABM cắt tia OB tại giao điểm thứ 2 là N; đường tròn ngoại tiếp tam giác ACM cắt tia OC tại giao điểm thứ 2 là P. Gọi I,J lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, MNP. Lấy E đối xứng với N qua OI. CMR: M,E,P,N cùng thuộc một đường tròn.
Giúp mình với! Cảm ơn!
Cho tam giác ABC cân tại A và M là một điểm nằm bên trong tam giác ABC sao cho góc AMB lớn hơn góc AMC . Chứng minh : DC = MB, BM< MC
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
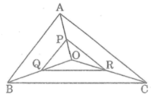
* Trong △ AOB ta có:
P trung điểm của OA (gt)
Q trung điếm của OB (gt)
Suy ra PQ là đường trung bình của △ AOB
Suy ra: PQ = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 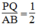 (1)
(1)
* Trong △ OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra PR là đường trung bình của tam giác OAC.
Suy ra: PR =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 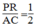 (2)
(2)
* Trong △ OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra QR là đường trung bình của tam giác OBC
Suy ra: QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 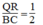 (3)
(3)
Từ (1), (2) và (3) suy ra: 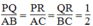
Vậy △ PQR đồng dạng △ ABC (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A (1;2), B (-3; -1), và C (3; -4). Tìm điều kiện của tham số m để điểm M (m; \(\dfrac{m-5}{3}\)) nằm bên trong tam giác ABC.
cho tam giác ABC và điểm O nằm trong tam giác đó chứng minh OA+OC<BA+BC















