ta có hệ phương trình:
2p+n=40
n-p=1
(giúp mình giải hệ phương trình này với)
(đề là tính p,e,n)
Những câu hỏi liên quan
có hệ phương trình,gồm:
2p+n=40
n-p=1
(giúp mình giải hệ phương trình này với) (đề bài là tìm số electron,proton và notron)
\(\left\{{}\begin{matrix}2p+n=40\\n-p=1\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}p=e=13\\n=14\end{matrix}\right.\)
Vậy số electron là 13 hạt, số proton là 13 hạt, số notron là 14 hạt
Đúng 0
Bình luận (0)
giúp mình giải hệ phương trình câu này với
Đọc tiếp
giúp mình giải hệ phương trình câu này với
Cho hệ phương trình: { 2mx + y 2 (m mà than số) { 8x + my m + 2a) Giải hệ phương trình khi m -1b) Tìm m để hệ phương trình có nghiệm là x 2; y 6c) Giải và biện luận hệ phương trình theo md) Trong trường hợp có nghiệm duy nhất:+ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m+ Tìm m để 4x + 3y 7+ Tìm m để x - y 0 + Tìm m để P y^2 - 2x đạt giá trị nhỏ nhất
Đọc tiếp
Cho hệ phương trình: { 2mx + y = 2 (m mà than số)
{ 8x + my = m + 2
a) Giải hệ phương trình khi m = -1
b) Tìm m để hệ phương trình có nghiệm là x = 2; y = 6
c) Giải và biện luận hệ phương trình theo m
d) Trong trường hợp có nghiệm duy nhất:
+ Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc m
+ Tìm m để 4x + 3y = 7
+ Tìm m để x - y > 0
+ Tìm m để P = y^2 - 2x đạt giá trị nhỏ nhất
GIÚP MÌNH GIẢI BÀI NÀY VỚI Ạ
ĐỀ : GIẢI CÁC HỆ PHƯƠNG TRÌNH SAU
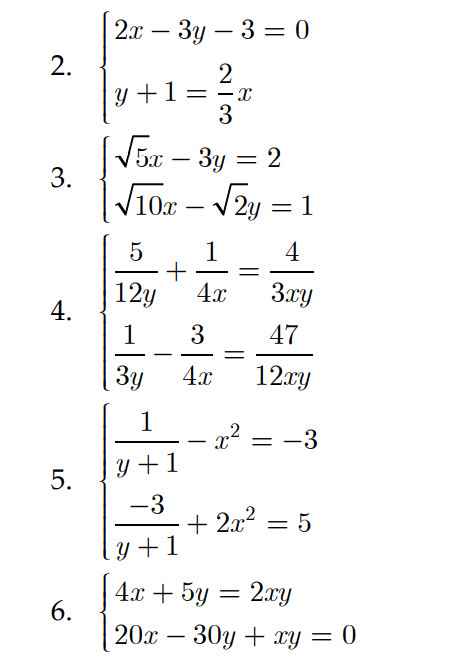
1/x + 1/y =5/18 và y/3x + x/3y =13/18 ai giải giúp mình hệ phương trình này với mình cần gấp!!!
giải hệ phương trình này giúp mình vs
Đọc tiếp
giải hệ phương trình này giúp mình vs
\(\left\{{}\begin{matrix}x+y=5\\\dfrac{3}{5}+\dfrac{2}{x-y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\\dfrac{2}{x-y}=\dfrac{12}{5}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+y=5\\6\left(x-y\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\x-y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{35}{6}\\y=x-\dfrac{5}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{35}{12}\\y=\dfrac{25}{12}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho hệ phương trình \(|^{mx+2y=1}_{3x+\left(m+1\right)y=-1}\) (với m là tham số)
a) Giải hệ phương trình với m = 3.
b) Giải và biện luận hệ phương trình theo m.
c) Tìm m để hệ phương trình có nghiệm là số nguyên.
Cho phương trình: x2-2(m-1)x-m-3=0 (1)
a) giải phương trình với m=-3
b) tìm m để phương trình (1) có 2 nghiệm thỏa mãn hệ thức x21 + x22 =10
c) tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc giá trị của m
Mn giúp mình với,mình cần gấp phần a mình làm đc rồi mn giúp mình phần b,c
b, \(\Delta'=b'^2-ac=\left[-\left(m-1\right)\right]^2-1.\left(-m-3\right)=m^2-2m+1+m+3\)
\(=m^2-m+4=m^2-m+\frac{1}{4}+\frac{15}{4}=\left(m-\frac{1}{2}\right)^2+\frac{15}{4}>0\)
Vậy pt (1) có 2 nghiệm x1,x2 với mọi m
Theo hệ thức vi-et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\left(2\right)\\x_1x_2=-m-3\left(3\right)\end{cases}}\)
Ta có: \(x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>\(4\left(m-1\right)^2-2\left(-m-3\right)=10\)
<=>\(4m^2-8m+4+2m+6=10\)
<=>\(4m^2-6m+10=10\Leftrightarrow2m\left(2m-3\right)=0\)
<=>\(\orbr{\begin{cases}m=0\\m=\frac{3}{2}\end{cases}}\)
c, Từ (2) => \(m=\frac{x_1+x_2+2}{2}\)
Thay m vào (3) ta có: \(x_1x_2=\frac{-x_1-x_2-2}{2}-3=\frac{-x_1-x_2-8}{2}\)
<=>\(2x_1x_2+x_1+x_2=-8\)
Cho hệ phương trình \(\left\{{}\begin{matrix}x+my=4\\nx+y=-3\end{matrix}\right.\)
a.Tìm m,n để hệ phương trình có nghiệm là (x ; y) = (-2 ; 3)
b.Tìm m,n để hệ phương trình có vô số nghiệm
\(a,\text{Thay }x=-2;y=3\\ HPT\Leftrightarrow\left\{{}\begin{matrix}3m-2=4\\3-2n=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\n=3\end{matrix}\right.\\ b,HPT\Leftrightarrow\left\{{}\begin{matrix}x=4-my\\n\left(4-my\right)+y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4-my\\4n-mny+y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=4-my\\y\left(mn-1\right)=4n+3\end{matrix}\right.\)
HPT có vô số nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}mn-1=0\\4n+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{4}{3}\\n=-\dfrac{3}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)