ko bt ae

đâu

:) vẫn như bth :>

Bài 1: Tìm n∈Nn∈N sao cho 2n−1⋮72n−1⋮7
Giải:
Nếu n=3k(k∈N)n=3k(k∈N) thì 2n−1=23k−1=8k−1⋮72n−1=23k−1=8k−1⋮7
Nếu n=3k+1(k∈N)n=3k+1(k∈N) thì 2n−1=23k+1−1=2(23k−1)+1=7m+12n−1=23k+1−1=2(23k−1)+1=7m+1
Nếu n=3k+2(k∈N)n=3k+2(k∈N) thì 2n−1=23k+2−1=4(23k−1)+3=7m+32n−1=23k+2−1=4(23k−1)+3=7m+3
Vậy: 2n−1⋮72n−1⋮7khi n = BS 3
Bài 2: Tìm n ∈ N để:
a)3n−1⋮8a)3n−1⋮8
b)A=32n+3+24n+1⋮25b)A=32n+3+24n+1⋮25
c)5n−2n⋮9c)5n−2n⋮9

Giải:

a) Khi n = 2k (k ∈ N) thì 3ⁿ – 1 = 3^2k – 1 = 9^k – 1 chia hết cho 9 – 1 = 8
Khi n = 2k + 1 (k ∈ N) thì 3ⁿ – 1 = 3^{2k + 1}  – 1 = 3. (9^k – 1 ) + 2 = BS 8 + 2
Vậy : 3ⁿ – 1 chia hết cho 8 khi n = 2k (k ∈ N)
b) A = 3^{2n + 3} + 2^{4n + 1} = 27 . 3²ⁿ + 2.2⁴ⁿ =  (25 + 2) 3²ⁿ  + 2.2⁴ⁿ = 25. 3²ⁿ  + 2.3²ⁿ  + 2.2⁴ⁿ
= BS 25 + 2(9ⁿ  + 16ⁿ)
Nếu n = 2k +1(k ∈ N) thì 9ⁿ  + 16ⁿ = 9^{2k + 1} + 16^{2k + 1} chia hết cho 9 + 16 = 25
Nếu n = 2k  (k ∈ N) thì 9ⁿ có chữ số tận cùng bằng 1 , còn 16ⁿ có chữ số tận cùng bằng 6
suy ra 2((9ⁿ  + 16ⁿ) có chữ số tận cùng bằng 4 nên A không chia hết cho 5 nên không chia hết cho 25
c) Nếu n = 3k (k ∈ N) thì 5ⁿ – 2ⁿ = 5^3k – 2^3k chia hết cho 5³ – 2³ = 117 nên chia hết cho 9
Nếu n = 3k + 1 thì 5ⁿ – 2ⁿ =  5.5^3k – 2.2^3k = 5(5^3k – 2^3k) + 3. 2^3k = BS 9 + 3. 8^k
= BS 9 + 3(BS 9 – 1)^k = BS 9 + BS 9 + 3
Tương tự:  nếu n = 3k + 2 thì 5ⁿ – 2ⁿ không chia hết cho 9

Dạng 2: Tìm điều kiện chia hết

Ví dụ 1: Tìm số nguyên n để giá trị của biểu thức A chia hết cho giá trị của biểu thức B:
A=n3+2n2−3n+2,B=n2−nA=n3+2n2−3n+2,B=n2−n
Giải: Đặt tính chia:

Muốn chia hết, ta phải có 2 chia hết cho n(n-1),do đó 2 chia hết cho n(vì n là số nguyên)
Ta có:

Vậy n= -1; n = 2
Ví dụ 2:
Tìm số nguyên dương n để n5+1⋮n3+1.n5+1⋮n3+1.
Giải: Ta có
n5+1⋮n3+1⇔n2(n3+1)−(n2−1)⋮(n+1)(n2−n+1)⇔(n−1)(n+1)⋮(n+1)(n2−n+1)⇔n−1⋮n2−n+1(n+1≠0)n5+1⋮n3+1⇔n2(n3+1)−(n2−1)⋮(n+1)(n2−n+1)⇔(n−1)(n+1)⋮(n+1)(n2−n+1)⇔n−1⋮n2−n+1(n+1≠0)

Nếu n =1 thì ta được 0 chia hết cho 1
Nếu n>1 thì n−1<n(n−1)+1=n2−n+1n−1<n(n−1)+1=n2−n+1, do đó không thể chia hết cho n2−n+1.n2−n+1.

Vậy giá trị duy nhất của n tìm được là 1.
Ví dụ 3:
Tìm số nguyên n để n5+1⋮n3+1.n5+1⋮n3+1.
Giải: Theo ví dụ trên ta có:
n−1⋮n2−n+1⇒n(n−1)⋮n2−n+1⇒n2−n⋮n2−n+1⇒(n2−n+1)−1⋮n2−n+1⇒1⋮n2−n+1n−1⋮n2−n+1⇒n(n−1)⋮n2−n+1⇒n2−n⋮n2−n+1⇒(n2−n+1)−1⋮n2−n+1⇒1⋮n2−n+1
Có hai trường hợp
n2−n+1=1⇔n(n−1)=0⇔n=0;n=1.n2−n+1=1⇔n(n−1)=0⇔n=0;n=1. Các giá trị này thoả mãn đề bài.
n2−n+1=−1⇔n2−n+2=0n2−n+1=−1⇔n2−n+2=0   Không tìm được giá trị của n
Vậy n= 0; n =1 là hai số phải tìm.
Ví dụ 4:
Tìm số tự nhiên n sao cho 2n−1⋮7.2n−1⋮7.
Giải:
Nếu n = 3k (k ∈ N) thì 2ⁿ -1 = 2^3k -1 = 8^k -1
Chia hết cho 7
Nếu n =3k +1(k ∈ N) thì
2ⁿ -1= 2^3k+1 – 1=2(2^3k -1) +1 = Bs 7 +1
Nếu n = 3k +2 ( k ∈ N) thì
2ⁿ -1= 2^3k+2 -1 =4(2^3k – 1)+3 =Bs 7 +3
Vậy 2ⁿ -1 chia hết cho 7 n = 3k(k ∈ N).

*Bài tập áp dụng

Bài 1: Tìm điều kiện của số tự nhiên a để a2+3a+2⋮6a2+3a+2⋮6
Giải:
Ta có a2+3a+2=(a+1)(a+2)a2+3a+2=(a+1)(a+2) là tích của 2 số tự nhiên liên tiếp nên chia hết cho 2
Do đó a2+3a+2⋮3⇔a2+2⋮3⇔a2=3k+1⇔a⋮̸3.a2+3a+2⋮3⇔a2+2⋮3⇔a2=3k+1⇔a⋮̸3.

Điều kiện phải tìm là a không chia hết cho 3.
Bài 2:
Tìm điều kiện của số tự nhiên a để a4−1⋮240.a4−1⋮240.

Bài 3:
Tìm số nguyên tố p để 4p +1 là số chính phương.
Bài 4.
Tìm ba số nguyên tố liên tiếp a,b,c sao cho a2+b2+c2a2+b2+c2  cũng là số nguyên tố
Giải: Xét hai trường hợp
+ Trong 3 số a,b,c có một số bằng 3.
Khi đó 22+32+52=3822+32+52=38 là hợp số (loại)
Còn 32+52+72=8332+52+72=83 là số nguyên tố.
+ Cả 3 số a,b,c đều lớn hơn 3.
Khi đó a2,b2,c2a2,b2,c2 đều chia cho 3 dư 1 nên
a2+b2+c2a2+b2+c2 chia hết cho 3,là hợp số (loại)
Vây ba số phải tìm là 3,5,7.
* Các bài tập tổng hợp các dạng toán trên
Bài 1. Cho các số nguyên a,b,c đều chia hết cho 6. Chứng minh rằng
Nếu a+ b+ c chia hết cho 6 thì a3+b3+c3⋮6a3+b3+c3⋮6

Bài 2: Chứng minh rằng tổng các lập phương của ba số nguyên liên tiếp thì chia hết cho 9.
Bài 3: Chứng minh rằng A chia hết cho B với
A=13+23+33+…+993+1003B=1+2+3+…+99+100.A=13+23+33+…+993+1003B=1+2+3+…+99+100.

Bài 4. Chứng minh rằng nếu các số tự nhiên a,b,c thoả mãn điều kiện
a2+b2=c2a2+b2=c2 thì abc chia hết cho 60.

Dạng 3: Tìm số dư

Ví dụ 1: Tìm số dư khi chia 21002100
a) cho 9;            b) cho 25;           c) cho 125.
Giải:
a) Lũy thừa của 2 sát với một bội số của 9 là 2³ = 8 = 9-1
Ta có 2¹⁰⁰ =2( 2³)³³ = 2(9-1)³³=2(B(9-1))
= B( 9) -2= B(9)+ 7
Số dư khi chia 2¹⁰⁰ cho 9 là 7.
b) Lũy thừa của 2 sát với bội số của 25 là
2¹⁰ = 1024 =B(25) -1
Ta có  2¹⁰⁰= (2¹⁰)¹⁰ =(B(25) -1)¹⁰ =B(25) +1
Số dư khi chia 2¹⁰⁰ cho 25 là 1.
c) Dùng công thức Niu-tơn:
2¹⁰⁰ = (5 – 1)⁵⁰ =5⁵⁰-50.50⁴⁹+….+-50.5+1.
Không kể phần hệ số của khai triển Niu-tơn thì 48 số hạng đầu đã chứa lũy thừa của 5 với sô mũ lớn hơn hoặc bằng 3 nên chia hết  cho 125, số hạng cuối là 1 .
Vậy 2¹⁰⁰ chia cho 125 dư 1.

Ví dụ 2: Tìm ba chữ số tận cùng của 2¹⁰⁰ khi viết trong hệ thập phân.
Giải: Theo ví dụ trên ta có
2¹⁰⁰ = BS 125 +1,mà 2¹⁰⁰ là số chẵn, nên ba chữ số tận cùng của nó chỉ có thể là 126, 376, 626 hoặc 876.
Mà 2¹⁰⁰ chia hết cho8 nên ba chữ số tận cùng của nó phải chia hết cho 8.Trong 4 số trên chỉ có 376 thoả mãn điều kiện này.
Vậy ba chữ số tận cùng của 2¹⁰⁰ là 376.
Chú ý: Nếu n là số chẵn không chia hết cho 5 thì 3 chữ số tận cùng của n¹⁰⁰ là 376.
Ví dụ 3: Tìm 4 chữ số tận cùng của 5¹⁹⁹⁴ viết trong hệ thập phân.
Giải: 
Cách 1. Ta thấy số tận cùng bằng 0625 nâng lên luỹ thừa nguyên dương bất kì vẫn tận cùng bằng 0625.Do đó
5¹⁹⁹⁴=5^4k+2 =25(5^4k)=25(0625)^k
= 25.(…0625)  = …..5625
Cách 2. Ta thấy 5^4k -1 chia hêt cho 5⁴ -1
= (5² -1)(5² +1) nên chia hết cho 16.
Ta có: 5¹⁹⁹⁴ = 5⁶( 5³³² -1) +5⁶
Do 5⁶ chia hết cho 5⁴, còn 5³³² -1 chia hết cho 16 nên 5⁶( 5³³² -1) chia hết cho 10000
Và 5⁶ = 15625.
Vậy 4 chữ số tận cùng của 5¹⁹⁹⁴ là 5
Bài tập tương tự
1.CMR với mọi số tự nhiên n thì 7ⁿ và 7ⁿ⁺⁴ có hai chữ số tận cùng như nhau.
+ Cho hs đặt câu hỏi: Khi nào hai số có hai chữ số tận cùng giống nhau?
– Khi hiệu của chúng chia hết cho 100
  Giải: Xét hiệu của 7^{n +4}– 7ⁿ = 7ⁿ( 7⁴ -1)
= 7ⁿ .2400
Do đó 7ⁿ⁺¹ và 7ⁿ có chữ số tận cùng giống nhau.
2.Tìm số dư của 22²²+55⁵⁵ cho 7.
+ Xét số dư của 22 và 55 cho 7?
Giải: Ta có  22²² + 55⁵⁵ =(B(7) +1)²² +(B(7) -1)⁵⁵
                                                               = B(7) +1+ B(7) -1
= B(7)
Vậy22²² + 55⁵⁵ chia hết cho 7

Thanks bạn nhều

):< no

thanks

Ủa sao bạn mất nick ???

chắc thế đó anh

BN TRA TRÊN INTERNET  LÀ OK LUÔN

Trung học phổ thông Chu Văn An.

Trung học Phổ Thông Chu Văn An

Trung học phổ thông Chu Văn (THPT Chu Văn An)

Còn cần ko nhỉ, mấy câu này cơ bản áp dụng công thức thôi mà?

1. "Ví của tôi" hoạt động như thế nào?

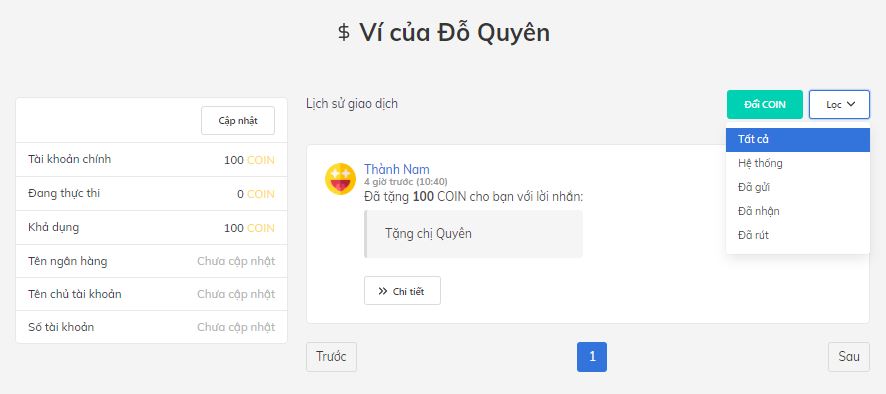
Khi vào ví của mình, các bạn sẽ thấy COIN, 1 COIN = 1000 VNĐ. Các bạn có thể rút COIN bằng cách gửi yêu cầu chuyển tiền về tài khoản ngân hàng, hoặc đổi ra thẻ điện thoại. Chỉ có thể rút COIN khi số COIN trong tài khoản khả dụng từ 50 trở lên. 

Lưu ý: Tên ngân hàng, tên chủ tài khoản, số tài khoản và số điện thoại cần cập nhật chính xác để hệ thống có thể chuyển tiền/thẻ điện thoại cho bạn.

Trong lịch sử giao dịch, các bạn có thể kiểm tra trạng thái nhận, gửi, rút COIN của mình.

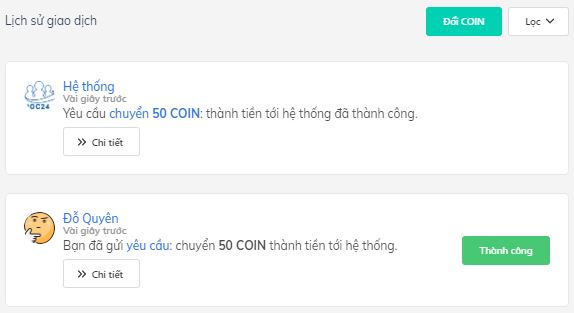
Ngoài ra, các bạn có thể tặng COIN từ ví của mình cho tài khoản của bạn khác nữa nhé.

2. Làm sao để được COIN?

Hiện tại, có năm cách để được COIN trong "ví của tôi".

- Trả lời hỏi đáp nhanh nhất và được giáo viên tick đúng 2GP.

Câu trả lời đúng đưa ra trong vòng 20 phút sau câu hỏi sẽ được cộng 2 COIN.

Câu trả lời đúng đưa ra trong vòng 20-40 phút sau câu hỏi sẽ được cộng 1 COIN.

Giáo viên, CTV chỉ tick một câu trả lời đúng nhất, sớm nhất, trình bày đẹp nhất cho mỗi câu hỏi. Không tick câu trả lời copy.

- Đóng góp nội dung cho Hoc24.

Trong nội dung lí thuyết của các bài học, có chức năng "các phiên bản chỉnh sửa", với những bài học chưa có nội dung (đặc biệt phần Soạn văn, Tập làm văn mẫu), các bạn có thể vào tạo nội dung, giáo viên sẽ duyệt, hiện thị nội dung đó và tặng coin xứng đáng với bài đóng góp.

Nếu bạn nào copy từ các trang khác bị nhắc nhở quá 3 lần sẽ bị khóa chức năng này.

- Được giải thưởng tuần (50 COIN).

- Được thăng hạng GP (từ thiếu tá lên trung tá: 10 COIN, trung tá lên thượng tá: 15 COIN, thượng tá lên đại tá: 20 COIN,...).

- Được người khác tặng.

Ngoài ra, các bạn có thể được thưởng COIN từ các cuộc thi; CTV, thành viên tích cực cuối mỗi kì.

3. COIN để làm gì?

Trước hết, COIN làm giàu "ví của tôi" để đổi ra tiền mặt/thẻ điện thoại. Đó là một phần thưởng và là sự ghi nhận của Hoc24 cho những đóng góp, cố gắng của các bạn.

COIN còn để tặng cho những bạn bè Hoc24 ở xa của mình kèm theo những lời nhắn nhủ, động viên.

Sau này, COIN còn có thể được dùng để mua các ấn phẩm, quà tặng của Hoc24 và nâng cấp tài khoản Hoc24 VIP.

Chúng ta hãy cùng trải nghiệm chức năng mới này và hoạt động tích cực để nhận được COIN một cách xứng đáng nhé!

 còn tui bị mắng là con ẩm ương

người ta ngủ mình chơi người ta chơi mình ngủ lại còn toàn học vào cái tầm nấu cơm nên bị mắng hoài