cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
giúp mình với
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
Cho góc nhọn xOy, trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi H là trung điểm của đoạn thẳng AB.
a) Chứng minh: ∆OAH = ∆OBH
b) Từ A vẽ đường thẳng vuông góc với OA, cắt tia OH tại C. Chứng minh: CB ⊥ OB.
c) Gọi I là trung điểm đoạn thẳng OH, từ I vẽ đường thẳng vuông góc với OH, cắt tia OA tại M. Kẻ HK vuông góc với BC tại K. Chứng minh: ba điểm M, H, K thẳng hàng.
có vẽ hình
a) Xét ΔOAHΔOAH và ΔOBHΔOBH ta có:
OA = OB (theo giả thiết)
HA = HB (H là trung điểm AB)
OH chung
⇒ΔOAH=ΔOBH(c−c−c)⇒ΔOAH=ΔOBH(c−c−c)
b) Ta có: ΔOAH=ΔOBHΔOAH=ΔOBH (chứng minh trên)
⇒∠AOH=∠BOH⇒∠AOH=∠BOH ( 2 góc tương ứng bằng nhau)
Hay ∠AOC=∠BOC∠AOC=∠BOC
Xét ΔOACΔOAC và ΔOBCΔOBC ta có:
OA = OB (theo giả thiết)
OC chung
∠AOC=∠BOC∠AOC=∠BOC
⇒ΔOAC=ΔOBC(c−g−c)⇒ΔOAC=ΔOBC(c−g−c)
⇒∠OAC=∠OBC⇒∠OAC=∠OBC(2 góc tương ứng)
Mà ∠OAC∠OAC= 900 nên ∠OBC∠OBC = 900
⇒CB⊥OB⇒CB⊥OB( điều phải chứng minh)
c) Ta có: ∠AOC=∠BOC∠AOC=∠BOC (chứng minh trên) (1)
Xét 2 tam giác vuông MIO và MIH ta có:
MI chung
IO = IH (Vì I là trung điểm của OH)
⇒ΔMIO=ΔMIH⇒ΔMIO=ΔMIH (Cạnh góc vuông – cạnh góc vuông)
⇒∠MOI=∠MHI⇒∠MOI=∠MHI (2 góc tương ứng)
Hay∠AOC=∠MHIHay∠AOC=∠MHI (2)
Từ (1) và (2) ta có: ∠BOC=∠MHI∠BOC=∠MHI (cặp góc ở vị trí so le trong)
⇒MH//OB⇒MH//OB (*)
Lại có:
HK⊥BCOB⊥BC}⇒HK//OBHK⊥BCOB⊥BC}⇒HK//OB (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**)
Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB.
Suy ra M, H, K thẳng hàng (điều phải chứng minh)
a) Xét tam giác AHO và tam giác BHO
có OH chung
HA=HB (GT)
OA=OB (GT)
suy ra tam giác AHO = tam giác BHO (c.c.c) (1)
b) Từ (1) suy ra góc AOC = góc BOC
Xét tam giác AOC và tam giác BOC có
OC chung
góc AOC = góc BOC
OA=OB (GT)
suy ra tam giác AOC = tam giác BOC (c.g.c)
suy ra góc OAC = góc OBC (hai góc tương ứng)
mà góc OAC =900
suy ra góc OBC = 900
suy ra CB vuông góc với OB tại B
Cho hai đường thẳng aa', bb' song song với nhau. Đường thẳng AB cắt aa', bb' lần lượt tại A, B. Tia phân giác của góc a'AB cắt bb' tại C.
a) Chứng minh : góc ABC = 2.góc ACB;
b) Tia phân giác của góc ABb' cắt aa' tại D. Chứng minh AC và BD vuông góc với nhau.
cho hình bình hành ABCD, qua C vẽ đường thẳng d chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' lần lượt là các đường vuông góc kẻ từ A,B,D đến d. chứng minh rằng AA' = BB'+DD'
Gọi O la giao điểm hai đường chéo hình bình hành
Từ O kẻ OO' vông góc với d tại O'
Ta có O' là trg điểm của A'O (do cùng vuông góc và song song với D' trên duog thẳng d )
suy ra OO'là dg trg bình cua tam giac AAC
suy ra AA' = 2 OO'(1)
Ta có DD' song song BB' ( do cùng vuông óc với d)
suy ra DD' ,BB' là hình thang
Ta có
OO' song song DD' song song BB' (cùng vuông góc d)(a)
Và O là trug điểm DB(b(
Từ (a) và(b) suy ra O là trung điểm D'B'
suy ra OO là dg2 trung bình của bình thang DD' BB'
suy ra OO' là dg trug bình của hình thang DD' BB'
suy ra D'B' =2OO' (2)
Từ (1) và (2) suy ra AA' =BB' +DD'
nhớ cho mình nha
bạn ơi đề bài sai rồi đánh lẽ phải là DD'=AA'+BB' chứ
b. Gọi I là giao của AA' với BH, chứng minh BH vuông góc với AA' tại I
c. chứng minh góc CHA= góc ABC
Biết HK vuông góc với bb' tại K
HK vuông góc với aa' tại H, cc' cắt aa' tại M, góc M1=\(45^o\), cc' cắt bb' tại N
a) Chứng minh aa' song song với bb'
b) Tính góc N1
c) Tia phân giác của góc HMN và tia phân giác của góc MNK cắt nhau tại I. Chứng minh MI vuông góc với IN
d) Chứng minh đường thẳng HK cắt đường thẳng cc'
đ) Gọi giao điểm của HK và cc' là E. Chứng minh tam giác KNE có 2 góc bằng nhau
cho hình bình hành ABCD. Kẻ đường thẳng a tiếp xúc với điểm D. Qua A, B, C hạ các đường thẳng AA', BB', CC' vuông góc vs đường thẳng a. Chứng minh: BB'=AA'+CC'
bn vô các câu hỏi tương tự có đầy đó bn
Cho hình hình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng minh rằng AA' = BB' + DD'
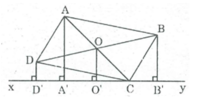
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
Cho hình lập phương ABCD.A'B'C'D' như hình vẽ.
a) Nêu vị trí tương đối của các cặp đường thẳng BC' và A'D'; DD' và AB; AA’ và A’C'.
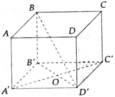
b) Chứng minh A'C' vuông góc với (BB'D'). Từ đó chứng minh A'C' vuông góc BD'.
c) Chứng minh B O = B B ' + 1 4 B ' A ' 2 + B ' C ' 2