chứng minh định lí Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.

Những câu hỏi liên quan
Cho định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
-Chứng minh định lí trên
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
Đúng 2
Bình luận (2)
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
Đúng 3
Bình luận (1)
Chứng minh :
\(\widehat{mOz=\frac{1}{2}}\widehat{xOz}\) \(\left(1\right)\) ( vì Om là hai tia phân giác của \(\widehat{xOz}\) )
\(\widehat{zOn}=\frac{1}{2}\widehat{zOy}\) \(\left(2\right)\) ( vì On là hai tia phân giác của \(\widehat{zOy}\) )
Từ \(\left(1\right)\) và \(\left(2\right)\) , ta có :
\(\widehat{mOz}+\widehat{zOn}=\frac{1}{2}.\left(\widehat{xOz}+\widehat{zOy}\right)\) \(\left(3\right)\)
Vì tia \(Oz\) nằm giữa hai tia \(Om,On\) và vì \(\widehat{xOz}\) và \(\widehat{zOy}\) kề bù \(\left(gt\right)\)
Nên từ \(\left(3\right)\) \(\Rightarrow\widehat{mOn}=\frac{1}{2}.180^0\)
Hay \(\widehat{mOn}=90^0\)
Đúng 2
Bình luận (2)
Chứng minh rằng góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Xem thêm câu trả lời
chứng minh định lí:
góc tạo bởi 2 tia phân giác của hai góc kề bù bằng 90 độ
Ta có: \(\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}\) (vì Om là tia phân giác của xOz)
\(\widehat{zOn}=\widehat{nOy}=\frac{\widehat{yOz}}{2}\) (vì On là tia phân giác của yOz)
Có: \(\widehat{mOn}=\widehat{mOz}+\widehat{zOn}=\frac{\widehat{xOz}}{2}+\frac{\widehat{yOz}}{2}=\frac{\widehat{xOz}+\widehat{yOz}}{2}=\frac{180^o}{2}=90^o\)
=> Om _|_ On (đpcm)
Đúng 0
Bình luận (0)
mOz=12ˆxOzˆmOz=12^xOz^ (1)(1) ( vì Om là hai tia phân giác của xOzˆxOz^ )
zOnˆ=12zOyˆzOn^=12zOy^ (2)(2) ( vì On là hai tia phân giác của zOyˆzOy^ )
Từ (1)(1) và (2)(2) , ta có :
mOzˆ+zOnˆ=12.(xOzˆ+zOyˆ)mOz^+zOn^=12.(xOz^+zOy^) (3)(3)
Vì tia OzOz nằm giữa hai tia Om,OnOm,On và vì xOzˆxOz^ và zOyˆzOy^ kề bù (gt)(gt)
Nên từ (3)(3) ⇒mOnˆ=12.1800⇒mOn^=12.1800
Hay mOnˆ=900
Chứng minh định lí:
Hai tia phân giác của hai góc kề bù thì tạo thành góc vuông
Ta có \(A_1=A_2;A_3=A_4\)
Có \(A_1+A_2+A_3+A_4=180\)
\(\Rightarrow2\left(A_2+A_3\right)=180\)
\(\Rightarrow A_2+A_3=90\)
Đúng 1
Bình luận (0)
* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Đúng 1
Bình luận (0)
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
Fan TFboys phải không?...mình cũng vậy
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a, Cho định lí:Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
-hãy cho biết giả thiết của định lí
-hãy cho bik kết luận của định lí
- chứng minh định lí trên
Cảm ơn các bn nhìu lắm!
chứng minh định lí : hai tia phân giác của hai góc kề bù vuông góc với nhau
Cho định lí : Hai tia phân giác của hai góc kề bù tạo thành một góc vuông (hình vẽ). Gỉa thiết, kết luận của định lí là: A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD. Kết luận: OE⊥OF B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD. Kết luận: OE⊥OA C. Giả thiết: Cho góc bẹt AOB và tia OD.OE là phân giác góc BOD; OF là phân giác góc AOE. Kết luận: OE⊥OF D. Giả thiết: Cho góc bẹt AOBAOB và tia OD. OE là phân g...
Đọc tiếp
Cho định lí : "Hai tia phân giác của hai góc kề bù tạo thành một góc vuông" (hình vẽ). Gỉa thiết, kết luận của định lí là:
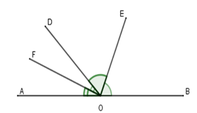
A. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
B. Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOF; OF là phân giác góc AOD.
Kết luận: OE⊥OA
C. Giả thiết: Cho góc bẹt AOB và tia OD.OE là phân giác góc BOD; OF là phân giác góc AOE.
Kết luận: OE⊥OF
D. Giả thiết: Cho góc bẹt AOBAOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AODAOD.
Kết luận: OB⊥OF
Đáp án C
Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF
Đúng 1
Bình luận (0)
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy viết giả thiết và kết luận của định lí
Chứng minh định lí sau: Hai tia phân giác của một cặp góc kề bù thì vuông góc với nhau
Tham khảo nhé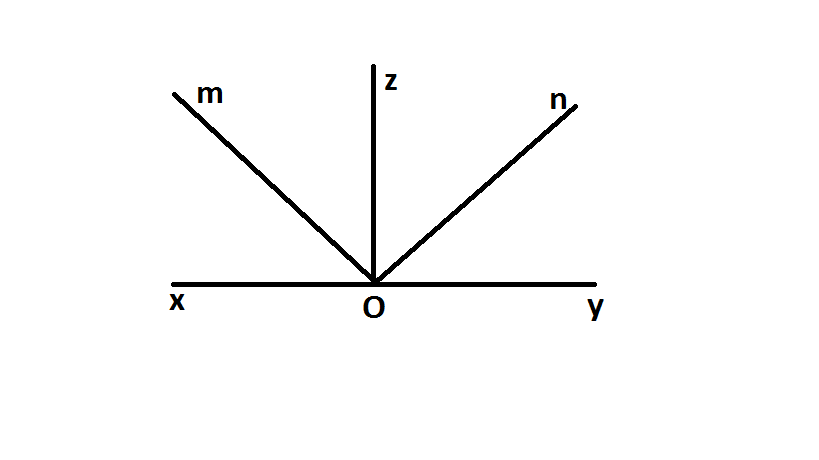
Ta có góc \(\widehat{\text{xOz}}\) + \(\widehat{\text{zOy}}\) = 180\(^o\)(kề bù)
=> 2(\(\widehat{mOz}\) +\(\widehat{zOn}\)) = 180\(^o\)
=> \(\widehat{mOz}\) + \(\widehat{zOn}\) = 90\(^o\)
=>\(\widehat{mOn}\) = 90\(^o\) (vì \(\widehat{xOz}\), \(\widehat{xOz}\) kề nhau)
=> Tia Om vuông góc tia On
Vậy 2 tia phân giác của 1 cặp góc kề bù thì vuông góc với nhau
Đúng 0
Bình luận (0)




























