Cho a, b là các số dương. Chứng tỏ:

Những câu hỏi liên quan
cho a,b,c là các số dương , chứng tỏ: a) a b + b a ≥ 2
\(\left(a-b\right)^2\ge0\)\(\Leftrightarrow a^2+b^2-2ab\ge0\)\(\Leftrightarrow a^2+b^2\ge0\)
\(\Rightarrow\frac{a^2+b^2}{ab}\ge\frac{2ab}{ab}\)\(\Leftrightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Đúng 0
Bình luận (0)
Sửa để: \(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\left(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right)^2\ge0\)
Đúng 0
Bình luận (0)
xl mk nhầm chỗ \(a^2+b^2\ge0\) phải là \(a^2+b^2\ge2ab\)
Đúng 0
Bình luận (0)
Cho a và b là các số dương, chứng tỏ: a b + b a ≥ 2 .
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b (*)
a > 0, b > 0 ⇒ a.b > 0 ⇒ 1/ab > 0
Nhân hai vế của (*) với 1/ab ta có:
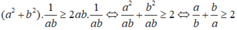
Đúng 0
Bình luận (0)
Cho a,b,c là các số nguyên dương. Chứng tỏ rằng: M= a/a+b + b/b+c + c/c+a không là số nguyên
Tham khảo:Câu hỏi của Tâm Lê Huỳnh Minh - Toán lớp 7 - Học trực tuyến OLM
Đúng 2
Bình luận (0)
Cho a, b, c, d là các số dương thỏa mãn a < b, c < d, chứng tỏ ac < bd.
Với a > 0, b > 0, c > 0, d > 0 ta có:
a < b ⇒ ac < bc (1)
c < d ⇒ bc < bd (2)
Từ (1) và (2) suy ra: ac < bd.
Đúng 0
Bình luận (0)
Cho a,b,c là các số nguyên dương. Chứng tỏ rằng: a/(a+b) + b/(b+c) + c/(c+a) không phải là số nguyên.
Cho a,b,c là các số nguyên dương. Hãy chứng tỏ rằng: D=(a/a+b)+(b/b+c)+(c/c+a) không phải là số nguyên
+ Vì a+ b + c > a + b => \(\frac{a}{a+b+c}
Đúng 0
Bình luận (0)
\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
\(1
Đúng 0
Bình luận (0)
Cho a;b;c là các số nguyên dương ,chứng tỏ rằng :
M=\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\)ko phải là một số nguyên dương.
Ta có:
\(\frac{a}{a+b}>\frac{a}{a+b+c}\)
\(\frac{b}{b+c}>\frac{b}{a+b+c}\)
\(\frac{c}{c+a}>\frac{c}{a+b+c}\)
\(\Rightarrow\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}\)
\(\Rightarrow M>\frac{a+b+c}{a+b+c}\)
\(\Rightarrow M>1\) (1)
Ta có:
\(\frac{a}{a+b}< 1\Rightarrow\frac{a}{a+b}< \frac{a+c}{a+b+c}\)
\(\frac{b}{b+c}< 1\Rightarrow\frac{b}{b+c}< \frac{a+b}{a+b+c}\)
\(\frac{c}{c+a}< 1\Rightarrow\frac{c}{c+a}< \frac{c+b}{a+b+c}\)
\(\Rightarrow\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< \frac{a+c}{a+b+c}+\frac{a+b}{a+b+c}+\frac{c+b}{a+b+c}\)
\(\Rightarrow M< \frac{2\left(a+b+c\right)}{a+b+c}\)
\(\Rightarrow M< 2\) (2)
Từ (1) và (2) => 1 < M < 2
=> M không phải là một số nguyên dương (đpcm)
Đúng 0
Bình luận (0)
áp dụng t/c dãy tỉ số bằng nhau, ta có
\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}=\frac{a+b+c}{a+b+b+c+c+a}=\frac{a+b+c}{\left(a+b+c\right)\cdot2}=\frac{ }{ }\)\(=\frac{1}{2}\)
=>Vậy nếu a;b;c>0->\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\)ko phải là 1 số nguyên dương
k cho mk
Đúng 0
Bình luận (0)
Cho a,b,c là các số nguyên dương chứng tỏ rằng :
M = \(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\) ko phải là 1 số nguyên dương.
\(\frac{a}{b+c}>\frac{a}{a+b+c},\frac{b}{b+c}>\frac{b}{b+c+a},\frac{c}{c+a}>\frac{c}{c+a+b}\)
\(\Rightarrow A>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
\(\frac{a}{a+b}< 1\Rightarrow\frac{a}{a+b}< \frac{a+c}{a+b+c},\frac{b}{b+c}< 1\Rightarrow\frac{b}{b+c}< \frac{b+a}{b+c+a},\frac{c}{a+a}< 1\Rightarrow\frac{c}{c+a}< \frac{c+b}{c+a+b}\)
\(\Rightarrow A< \frac{a+c}{a+b+c}+\frac{b+a}{a+b+c}+\frac{c+b}{c+a+b}=\frac{2\left(a+b+c\right)}{a+b+c}=2\)
Vậy \(1< A< 2\Rightarrow A\)không phải là một số nguyên dương
Đúng 0
Bình luận (0)
cho a;b;c là các số nguyên dương .Chứng tỏ [ a+b]/c+ [ b+c ] /a+ [c+a ]/b >hoăc =6
Cho a, b, c là các số nguyên dương. Chứng tỏ rằng
S =a/a + b + b/b+c + c/c + a> 1
a/a+b>a/a+b+c
b/b+c>b/a+b+c
c/c+a>c/a+b+c
Cộng hai vế của biểu thức
M>(a+b+c)/(a+b+c)=1
bạn làm đúng rồi nhé
chúc bạn học tốt@
Ta có: \(\hept{\begin{cases}\frac{a}{a+b}>\frac{a}{a+b+c}\\\frac{b}{b+c}>\frac{b}{a+b+c}\\\frac{c}{c+a}>\frac{c}{a+c+b}\end{cases}\Rightarrow\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}}\)
\(\Rightarrow S>\frac{a+b+c}{a+b+c}=1\left(đpcm\right)\)

























