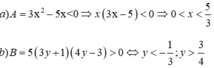Tìm x để biểu thức sau nhận giá trị âm

Những câu hỏi liên quan
tìm các giá trị nguyên x để biểu thức sau nhận giá trị âm A= x2-1/x2 -4x+3
a) Tìm giá trị của x để biểu thức
A
3
x
2
−
5
x
nhận giá trị âmb) Tìm giá trị của y để biểu thức
B
5
3
y
+
1
4
y
−
3
nhận giá trị dương.
Đọc tiếp
a) Tìm giá trị của x để biểu thức A = 3 x 2 − 5 x nhận giá trị âm
b) Tìm giá trị của y để biểu thức B = 5 3 y + 1 4 y − 3 nhận giá trị dương.
1. Tìm các giá trị của x để các biểu thức sau nhận giá trị âm:
a. x2 + 5x
b. 3(2x + 3)(3x - 5)
2. Tìm các giá trị của x để các biểu thức sau nhận giá trị dương:
a. 2y2 - 4y
b. 5(3y + 1)(4y - 3)
a,Tìm x để biểu thức :(x-3).(x+7) nhận giá trị dương
b,,Tìm x để biểu thức (2x+3).(3x-5) nhận giá trị âm
Ai giúp vs nè
1.Tìm giá trị của x biết :
\(\frac{x-7}{2}< 0\)
2. Xác định giá trị của x để biểu thức sau nhận giá trị âm : \(\frac{x+3}{x-5}\)
3.Tìm giá trị của x thuộc Z để biểu thức sau nhận giá trị dương
\(x^2+x\)
\(1.\frac{x-7}{2}< 0\)
\(\Leftrightarrow\frac{x-7}{2}.2< 0.2\)
\(\Leftrightarrow x-7< 0\Leftrightarrow x< 7\)
\(S=\left\{xlx< 7\right\}\)
2)\(\)Đề biểu thức sau nhân giá trị âm thì :
\(\frac{x+3}{x-5}< 0\Leftrightarrow x+3< 0\Leftrightarrow x< 3\left(Đk:x\ne5\right)\)
\(S=\left\{xlx< 3\right\}\)
3.Giá trị của x thuộc Z để biểu thức sau nhận giá trị dương:
\(x^2+x\ge0\)
\(\Leftrightarrow x\left(x+1\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}x\ge0\\x+1\ge0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge0\\x\ge-1\end{cases}}}\)
\(S=\left\{xlx\ge-1\right\}\)
Đúng 0
Bình luận (0)
1. tìm các giá trị của x để các biểu thức sau nhận giá trị âm:
a, x2+5x.
b,3(2x+3)(3x-5).
2.tìm các giá trị của y để các biểu thức sau nhận giá trị dương:
a, 2y2-4y.
b, 5(3y+1)(4y-3)
tìm các giá trị của x để các biểu thức sau nhận giá trị âm
Xem chi tiết
a) x2+5x
b) 3(2x+3) (3x-5)
bài 2. tìm các giá trị của x để biểu thức sau nhận giá trị dương
a)2y2-4y
b) 5(3y+1) (4y-3)
a, Để x2 + 5x đạt giá trị âm thì 1 trong 2 số là âm và GTTĐ của số âm hơn GTTĐ của số tư nhiên
và x2 luôn tự nhiên => 5x âm
=> GTTĐ của x2 < GTTĐ của 5x
=> x < 5
=> x thuộc {4; 3; 2; 1;....}
Vậy....
Đúng 0
Bình luận (0)
tìm x,y để biểu thức sau nhận giá trị âm 5.(3.y+1).(4.y-3)
tìm x,y để biểu thức sau nhận giá trị âm
B= 3(2y+3)(3y-5)
\(B=3\left(2y+3\right)\left(3y-5\right)\)là sô âm
\(\Rightarrow B< 0\)tức \(3\left(2y+3\right)\left(3y-5\right)< 0\)
để \(3\left(2y+3\right)\left(3y-5\right)< 0\)thì \(3;2y+3;3y-5\ne\)dấu
th1\(\hept{\begin{cases}3>0\\2y+3< 0\\3y-5>0\end{cases}\Leftrightarrow\hept{\begin{cases}3>0\\2y< -3\\3y>5\end{cases}}\Leftrightarrow\hept{\begin{cases}3>0\\y< \frac{-3}{2}\\y>\frac{5}{3}\end{cases}}\Rightarrow\frac{5}{3}< y< \frac{-3}{2}\left(l\right)}\)
th2\(\hept{\begin{cases}3>0\\2y+3>0\\3y-5,0\end{cases}\Leftrightarrow\hept{\begin{cases}3>0\\2y>-3\\3y< 5\end{cases}}\Leftrightarrow\hept{\begin{cases}3>0\\y>\frac{-3}{2}\\y< \frac{5}{3}\end{cases}}\Rightarrow\frac{-3}{2}< y< \frac{5}{3}\left(tm\right)}\)
=>.....
hình như đề sai
Đúng 0
Bình luận (0)
Xem thêm câu trả lời