Chứng minh rằng : Nếu 2 đường cao của một tam giác bằng 12 và 20 thì đường cao thứ 3 nhỏ hơn 30 (sử dụng BĐT tam giác)

Những câu hỏi liên quan
Chứng minh rằng nếu bán kính đường tròn nội tiếp của một tam giác bằng ì đường cao lớn nhất của tam giác đó không nhỏ hơn 1.
( giúp Được thì Giúp mình Nha! )
Chứng minh rằng một tam giác có hai cạnh không bằng nhau thì tổng của cạnh lớn hơn và đường cao tương ứng lớn hơn tổng của cạnh nhỏ và đường cao tương ứng
vì trong 1 tam giác chỉ có 1 đường cao chung
mà 1 cạnh dài,1 cạnh ngắn
nếu cộng thêm đường cao vào vs cạnh dài hơn
và cộng đường cao vào vs cạnh ngắn hơn
thì đương nhiên ta đã ra điều phải chứng minh rùi
mình k giỏi lập luận nên lấy ví dụ cho dẽ hiểu nè:
giả sử đường cao=2cm,cạnh dài=6cm,cạnh ngắn=4cm
tổng đường cao và cạnh dài:2+6=8
tổng đường cao và cạnh ngắn:2+4=6
đều có chung 2,6>4
=>điều phải chứng minh
Đúng 0
Bình luận (0)
a) nếu một tam giác có độ dài đương cao là 32 ; 52 và đường cao thứ 3 cũng là số chính phương thì đường cao thứ 3 là bao nhiêu
b) cho ba số nguyên tố lớn hơn 3 . Chứng minh rằng trong 3 số đó tồn tại hai số mà tổng hoặc hiệu của chúng chia hết cho 12
Chứng minh rằng: Trong một tam giác,đường phân giác ứng với cạnh lớn nhất thì nhỏ hơn hoặc bằng đường cao ứng với cạnh nhỏ nhất
Chứng minh rằng trong 1 tam giác có 2 cạnh ko bằng nhau thì tổng độ dài cạnh lớn hơn và đường cao tương ứng sẽ lớn hơn tổng độ dài cạnh nhỏ hơn và đường cao tương ứng
Ta giả sử AB < AC . Cần chứng minh AB + CH < AC + BK
Trên cạnh AC lấy điểm D sao cho AB = AD . Từ D lần lượt hạ các đường vuông góc với AB và AC lần lượt tại E và F.
Ta có tam giác ADE = tam giác ABK (đặc biệt) => DE = BK
Xét : \(AC+BK=AD+DC+CH=AB+CD+HF\)(Vì DEHF là hình chữ nhật => BK = DE = HF)
Mà trong tam giác vuông DFC có cạnh huyền CD nên ta có \(DC>CF\)
\(\Rightarrow AC+BK=AB+CD+HF>AB+CF+HF=AB+CH\)
Đúng 0
Bình luận (0)
HÌNH HỌC
1. Cho tam giác ABC có ^A = 600 . Kẻ các đường cao BD , CE . Gọi F là trung điểm của cạnh BC . Chứng minh tam giác DEF là tam giác đều
2. Chứng minh rằng trong một tam giác , chiều cao ứng với cạnh lớn hơn thì nhỏ hơn chiều cao ứng với cạnh nhỏ hơn
GỌI BN ,CM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
VÀ \(AB< AC\)
TA CÓ \(AB< AC\)
\(\Rightarrow\widehat{ACB}< \widehat{ABC}\)( QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN)
\(\Rightarrow BH< CK\)( QUAN HỆ GIỮA GÓC VÀ ĐƯỜNG XIÊN)
THEO ĐỀ
chiều cao ứng với cạnh lớn hơn thì nhỏ hơn chiều cao ứng với cạnh nhỏ hơn
\(BH< CK\left(TM\right)\)
NHẦM >>
\(\Rightarrow BN< CM\)
Ở DƯỞI CX ĐỔI NHA
Bài 2
*trình bày theo cách khác. Mượn hình bạn ミ★NVĐ^^★彡
Do AB>AC nên có thể lấy trên AB một điểm D sao cho AD=AC
Ta có \(\Delta ADC\)cân tại đỉnh A nên CK=DI (1)
Từ D kẻ DJ _|_ HB, vì D nằm giữa 2 điểm A,B nên điểm J phải nằm giữa 2 điểm H,B do vậy ta có: HJ<BH (2)
Mặt khác tứ giác DIHJ là hình chữ nhật nên DI=HJ (3)
Từ (1)(2)(3) => CK<BH
Xem thêm câu trả lời
Chứng minh:
1/ Trong một tam giác không thể có nhiều hơn một góc tù
2/ trong một tam giác, góc nhỏ nhất không thể lớn hơn 60 độ
3/ Tam giác ABC cân tại A, AM là dường trung tuyến của tam giác ABC. Chứng minh rằng AM cũng là đường cao, cũng là đường phân giác của tam giác ABC
1/Giả sử trong 1 tam giác có 2 hóc tù thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=>trong 1 tam giác chỉ có duy nhất 1 góc tù
2/Trong 1 tam giác nếu góc nhỏ nhất bằng 60 độ thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=> trong một tam giác góc nhỏ nhất không thể lớn hơn 60 độ
3/Xét tam giác AMB = tam giác AMC (c.c.c)
=> góc BMA = góc CMA
Mặt khác góc BMA + góc CMA = 180 độ
=> góc BMA = góc CMA = 90 độ
=> AM vuông góc BC
=> AM là đường cao của tam giác hạ từ đỉnh A
Tam giác BMA = tam giác CMA
=> góc BAM = góc CAM
=> AM là tia phân giác của góc A
Đúng 0
Bình luận (0)
Chứng minh rằng: Nếu một tam giác có hai đường cao bằng nhau thì nó là tam giác cân
hình bạn tự vẽ nhé ^^
giả sử giả thiết cho tam giác ABC có đường cao BF và CE (BF=CE)
xét tam giác EBC và tam giác FCB, có
góc BEC = góc BFC( =90 độ)
EC = BF (theo giả thiết)
BC chung
nên tam giác EBC= tam giácFBC ( cạnh huyền+cạnh góc vuông)
do đó góc ABC= góc ACB (2 góc tương ứng)
nên tam giác ABC cân tại A (đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng 1 tam giác có 2 đường cao (xuất phát từ các đỉnh của 2 góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra 1 tam giác có 3 đường cao bằng nhau là tam giác đều
Chứng minh phần " tam giác có 3 đường cao bằng nhau " giúp mình nha. Phần " tam giác có 2 đường cao bằng nhau " mình tự làm được
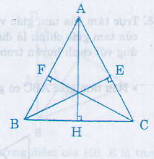
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Đúng 0
Bình luận (0)


















