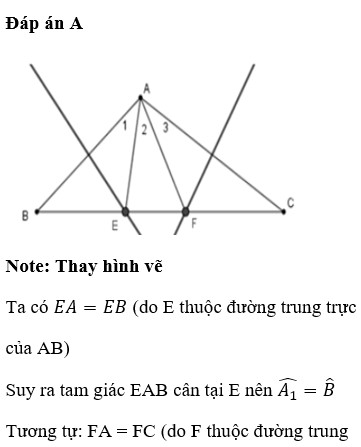
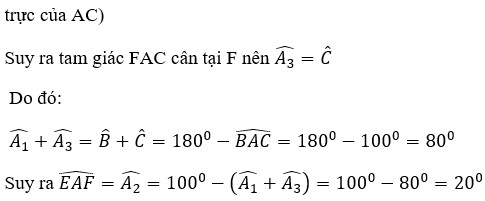Cho tam giác ABC có \(\widehat{A}=100^0\). Các đường trung trực của AB và AC lần lượt cắt BC ở E và F. Tính \(\widehat{EAF}\) ?
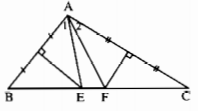
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC trong đó A ^ = 100 ° . Các đường trung trực của AB và AC cắt cạnh theo thứ tự tại E và F. Tính góc EAF
A. 20
B. 30
C. 40
D. 50
Cho tam giác ABC có A=110 độ . Các đường trung trực của AB và AC cắt BC theo thứ tự ở E và F . Tính EAF
mk chưa hok tới đường trung trực nên ko làm được sorry !!!!
5454654
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A=400 , BC là cạnh nhỏ nhất.Các đường trung trực của AB và AC cắt nhau ở I và cắt đường thẳng BC theo thứ tự ở E và F
a) CMR: FI là phân giác góc AFE,AEF
b) Tính góc FAE
các bạn làm nhanh giùm mình ná
Cho tam giác ABC trong đó có góc a=110 độ các đường trung trực của Ab và CD cắt cạnh BC theo thứ tự ở E và F. Tính góc EAF
Cho tam giác ABC có widehat{ABC}widehat{ACB}700 và đường cao AH. Các điểm E, F theo thứ tự thuộc các đoạn AH, AC sao cho widehat{ABE}widehat{CBF}300. Gọi M là trung điểm của AB.a) Chứng minh Delta AMFđồng dạng Delta BHEb) Chứng minh AB.BE BC. AE
Đọc tiếp
Cho tam giác ABC có \(\widehat{ABC}\)=\(\widehat{ACB}\)=700 và đường cao AH. Các điểm E, F theo thứ tự thuộc các đoạn AH, AC sao cho \(\widehat{ABE}\)=\(\widehat{CBF}\)=300. Gọi M là trung điểm của AB.
a) Chứng minh \(\Delta AMF\)đồng dạng \(\Delta BHE\)
b) Chứng minh AB.BE= BC. AE
Cho tam giác ABC vuông tại B và \(\widehat{ACB}=30^0\), tia phân giác góc A cắt cạnh BC tại D. Trên cạnh AC lấy E sao cho : AE = AB.
a) Tính số đo các góc\(\widehat{BAC},\widehat{ADC}\)
b) CM : \(\Delta ABD=\Delta AED\)
c) CM : DE là trung trực của đoạn AC
Bài làm
a) Xét ∆ABC vuông tại B có:
^BAC + ^C = 90°
Hay ^BAC + 30° = 90°
=> ^BAC = 60°
Vì AD là phân giác của góc BAC.
=> ^DAC = 60°/2 = 30°
Xét tam giác ADC có:
^DAC + ^ACD + ^ADC = 180°
Hay 30° + 30° + ^ADC = 180°
=> ^ADC = 180° - 30° - 30°
=> ^ADC = 120°
b) Xét tam giác ABD và tam giác AED có:
AB = AE ( gt )
^BAD = ^EAD ( Do AD phân giác )
Cạnh AD chung.
=> ∆ABD = ∆AED ( c.g.c )
c) Vì ∆ABD = ∆AED ( cmt )
=> ^ABD = ^AED = 90°
=> DE vuông góc với AC tại E (1)
Ta có: ^DAC = ^DCA = 30°
=> ∆DAC cân tại D.
=> AD = DC
Xét tam giác DEA và tam giác DEC có:
Góc vuông: ^DEA = ^DEC ( = 90° )
Cạnh huyền AD = DC ( cmt )
Góc nhọn: ^DAC = ^DCA ( cmt )
=> ∆DEA = ∆DEC ( g.c.g )
=> AE = EC
=> E là trung điểm của AC. (2)
Từ (1) và (2) => DE là trung trực của AC ( đpcm )
Cho tam giác ABC có \(\widehat{A}=60^0\). Các tia phân giác của các góc B, C cắt nhau ở I và cắt AC, AB theo thứ tự ở D, E. Chứng minh rằng ID = IE
Hướng dẫn : Kẻ tia phân giác của góc BIC
Tia phân giác của góc BIC cắt BC ở K. \(\Delta ABC\) có \(\widehat{A}=60^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^0-60^0=120^0,\widehat{B_1}+\widehat{C_1}=\dfrac{\widehat{B}+\widehat{C}}{2}=\dfrac{120^0}{2}=60^0.\)
\(\Delta BIC\) có \(\widehat{B_1}+\widehat{C_1}=60^0\Rightarrow\widehat{BIC}=180^0-60^0=120^0.\)
Suy ra \(\widehat{I_1}=60^0,\widehat{I_4}=60^0.\)
IK là tia phân giác của góc BIC nên \(\widehat{I_2}=\widehat{I_3}=60^0.\)
\(\Delta BIE = \Delta BIK\) (g.c.g) => IE = IK (2 cạnh tương ứng).
\(\Delta CID = \Delta CIK\)(g.c.g) => ID = IK (2 cạnh tương ứng).
Do đó ID = IE.
Đúng 0
Bình luận (0)
Cho
Δ
A
B
C
trong đó
A
^
100
0
. Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự tại E và F. Tính
E
A
F
^
A.
20
0
B.
30
0
C.
40
0
D.
50
0
Đọc tiếp
Cho Δ A B C trong đó A ^ = 100 0 . Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự tại E và F. Tính E A F ^
A. 20 0
B. 30 0
C. 40 0
D. 50 0
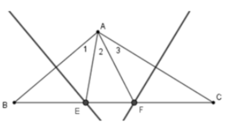
Ta có EA = EB (E thuộc đường trung trực của AB) nên tam giác EAB cân tại E
Suy ra A 1 ^ = B ^
Lại có FA = FC (do F thuộc đường trung trực của AC) nên tam giác FAC cân tại F
Suy ra A 3 ^ = C ^

Đúng 0
Bình luận (0)
Bài 1:Cho tam giác ABC có và BC6cma)Trên nửa mặt phẳng bờ là đường thẳng BC có chứa A vẽ tia Bx BC.Giải thích vì sao BA là tia phân giác của góc xBCb)Đường thẳng trung trực a của đoạn thẳng BC cắt các đường thẳng AB và AC tại E và F.Tính số đo của góc AEFc)Qua C vẽ đường thẳng song song với AB,đường thẳng này cắt đường thẳng a tại N.Tính số đo góc ACNd)So sánh 2 góc ENC và xBABài 2:Cho tam giác ABC có a)Tia phân giác của góc ABc cắt AC tại D.Qua A vẽ đường thẳng song song với BD,đường thẳng...
Đọc tiếp
Bài 1:Cho tam giác ABC có và BC=6cm
a)Trên nửa mặt phẳng bờ là đường thẳng BC có chứa A vẽ tia Bx BC.Giải thích vì sao BA là tia phân giác của góc xBC
b)Đường thẳng trung trực a của đoạn thẳng BC cắt các đường thẳng AB và AC tại E và F.Tính số đo của góc AEF
c)Qua C vẽ đường thẳng song song với AB,đường thẳng này cắt đường thẳng a tại N.Tính số đo góc ACN
d)So sánh 2 góc ENC và xBA
Bài 2:Cho tam giác ABC có
a)Tia phân giác của góc ABc cắt AC tại D.Qua A vẽ đường thẳng song song với BD,đường thẳng này cắt đường thẳng BC tại E.So sánh 2 góc BEA và BAE
b)Qua A vẽ đường thẳng xy song song BC.Tính số đo góc BAI
Bài 3:Cho tam giác ABC có
a)Hai tia phân giác của góc ABC và góc ACB cắt nhau tại I.Qua I vẽ đường thẳng song song với BC,đường thẳng này cắt các đường thẳng AB và AC tại D và E.Tính số đo góc ACI và góc CIE
b)So sánh 2 góc DIB và ABI
c)Qua A kẻ AH tại H,qua C kẻ CK
tại K.Giải thích vì sao AH//CK
d)Tính số đo góc CAH
Bài 8:Cho tam giác ABC có BC=8cm và
a)Qua A vẽ đường thẳng xy song song với BC(tia Ax thuộc nửa mặt phẳng bờ là đường thẳng AC có chứa điểm B).Tính số đo góc yAB và BAC
b)Vẽ AH tại H.Tính số đo các góc BAH và CAH
Bài 9:Cho tam giác ABC có BC=6cm,
a)Qua B kẻ tại D và
tại E,2 đường thẳng BD và CE cắt nhau tại H.Qua B và C lần lượt vẽ các đường thẳng vuông góc với AB và AC,2 đường thẳng này cắt nhau tại K.Vì sao CK//BD và BK//CE?
b)Tính số đo góc DBC
c)TÍnh số đo các góc HCB và EHD