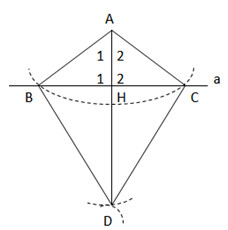
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi đó là điểm D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.

Những câu hỏi liên quan
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
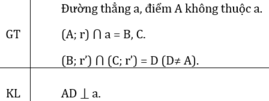
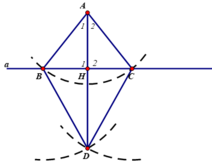
Gọi bán kính cung tròn tâm A là r, bán kính cung tròn tâm B và C là r’.
Xét ΔABD và ΔACD có:
AB = AC (=r)
DB = DC (=r')
AD cạnh chung
Nên ΔABD = ΔACD (c.c.c)
QUẢNG CÁO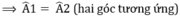
- Gọi H là giao điểm của AD và a
ΔAHB và ΔAHC có
AB = AC (= r)
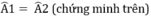
AH cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)

Đúng 0
Bình luận (0)
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B cà C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì saoAD vuông góc với đường thẳng a ?

Vì cung tròn tâm A cắt a ở B và C nên AB = AC. Mặt khác cung tâm B và C có cùng bán kính cắt nhau tại D nên DB = DC.
Xét ΔABD và ΔACD có :
AB = AC (gt)
BD = CD (gt)
AD là cạnh chung
ΔABD = ΔACD (c.c.c) ⇒∠A1 = ∠A2 (góc tương ứng)
Xét ΔAHB và ΔAHC có:
AB = AC (gt)
∠A1 = ∠A2 (c/m trên)
AH là cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)
⇒∠AHB = ∠AHC (góc tương ứng)
Mà ∠AHB +∠AHC = 180 độ ( 2 góc kề bù )
⇒ ∠AHB = ∠AHC = 90 độ
⇒ AD ⊥ a
Đúng 0
Bình luận (0)
cho điểm A NẰM NGOÀI ĐƯỜNG THẲNG a . Vẽ cung tròn tâm a cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. hãy giải thích vì sao AD vuông óc với đường thẳng a
∆ABD và ∆ACD có:
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
=> A1 = A2
Gọi H là giao điểm của AD và a.
∆AHB và ∆AHC có:
AB = AC (gt)
A1 = A2 ( cmt )
AH cạnh chung.
Nên ∆AHB = ∆AHC (c.g.c)
Suy ra: H1 = H2
Ta lại có:
H1 + H2 = 180
⇒H1 = H2 = 90
Vậy AD ⊥ a
P/s : Cứ nghĩ làm xong bài sẽ vẽ hình ai ngờ phần vẽ hình bị lỗi nên lại phải làm lại ( khóc hết nước mắt )
Giải
Xét ∆ABD và ∆ACD có :
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
\(\Rightarrow\) BAD = CAD ( 2 góc tương ứng )
Gọi H là giao điểm của AD và a
Xét ∆AHB và ∆AHC có :
AB = AC (gt)
BAH = CAH ( cmt )
AH cạnh chung
Nên ∆AHB = ∆AHC (c.g.c)
\(\Rightarrow\) AHB = AHC ( 2 góc tương ứng )
Ta lại có :
AHB + AHC = 180 ( 2 góc kề bù )
\(\Rightarrow\) AHB = AHC = 90
\(\Rightarrow\) AH ⊥ BC
\(\Rightarrow\) AD ⊥ a
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại 1 điểm khác A, gọi điểm đó là D. Giải thích vì sao AD vuông góc với đường thẳng a.
Cho điểm A nằm ngoài đuờng thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tân B và C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuống góc với đuờng thẳng a
Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm Acắt đường thẳng a ở Bvà C . Vẽ Các cung tròn tâm Bvà tâm C có cùng bán kính sao cho chúng cắt nhau tại 1 điểm khác A, gọi điểm đó là D . Hãy giải thích ví sao AD vuông góc với đường thẳng a
- Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a tại B và C. Vẽ các cung tròn B và C có cùng bán kình BA chúng cắt nhau tại D khác A. Giải thích vì sao AD vuông góc với a
Cho điểm A nằm ngoài đường thẳng a.Vẽ cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A,gọi điểm đó là D.Hỹ giải thích vì sao AD vuông góc với đường thẳng a
Cho điểm A nằm ngoài đường thẳng a . Vẽ cung tròn tâm A cắt đường thẳng a ở B và C . Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại mottj ddiiemr khác A , gọi điểm đó là D .Hayc giải thích vì sao AD vuông góc với đường thẳng a . Giúp mình với mình cần gấp trong tối hôm nay !
Đọc tiếp
Cho điểm A nằm ngoài đường thẳng a . Vẽ cung tròn tâm A cắt đường thẳng a ở B và C . Vẽ các cung tròn tâm B và tâm C có cùng bán kính sao cho chúng cắt nhau tại mottj ddiiemr khác A , gọi điểm đó là D .Hayc giải thích vì sao AD vuông góc với đường thẳng a .
Giúp mình với mình cần gấp trong tối hôm nay !