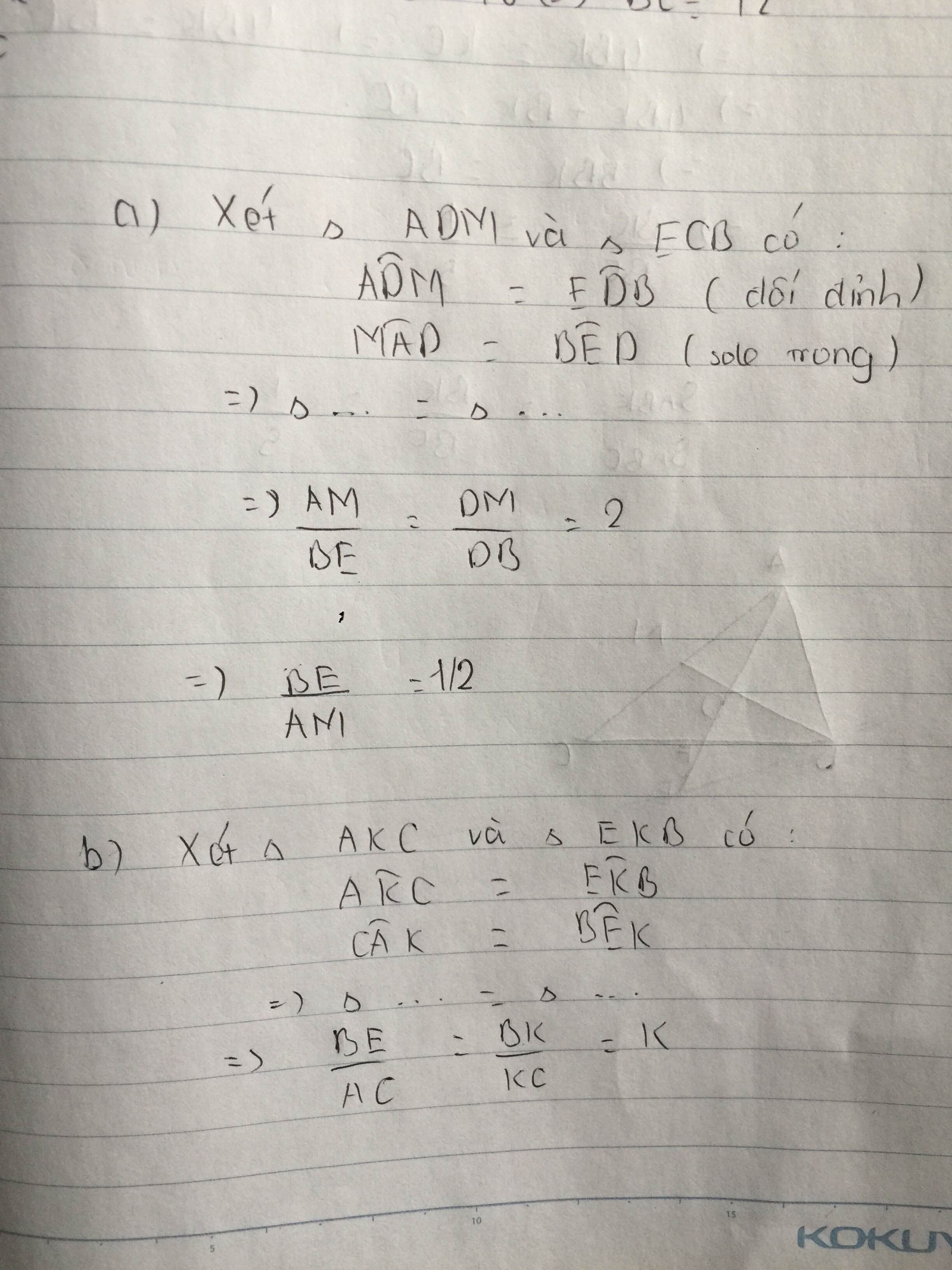Bài 1: cho ΔABC , vẽ ΔA'B'C' đồng dạng với ΔABC theo tỉ số đồng dạng k = 3/4.
Những câu hỏi liên quan
ΔABC ΔABC theo tỉ số đồng dạng k1, ΔABC ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác ABC đồng dạng với tam giác ABC theo tỉ số nào?
Đọc tiếp
ΔA'B'C'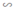 
ΔA''B''C'' theo tỉ số đồng dạng k1, ΔA''B''C''
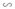ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
ΔA'B'C'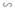 
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒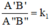 
ΔA''B''C''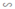 
ΔABC theo tỉ số đồng dạng k2 ⇒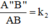 
Mà 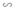ΔA'B'C' 
ΔA''B''C''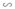; ΔA''B''C'' 
ΔABC
⇒ ΔA'B'C'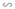 
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
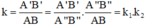
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
Đúng 0
Bình luận (0)
ΔA'B'C'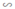 
ΔABC theo tỉ số đồng dạng k = 3/5.
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi của hai tam giác là 40dm, tính chu vi của mỗi tam giác.
a) Gọi chu vi tam giác A’B’C’ là P’ và chu vi tam giác ABC là P.
ΔA'B'C'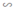 
ΔABC theo tỉ số đồng dạng k = 3/5
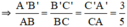
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
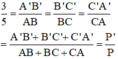
Vậy tỉ số chu vi tam giác A’B’C’ và tam giác ABC là 3/5
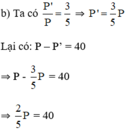
⇒ P = 100 ⇒ P’ = 60.
Vậy chu vi tam giác ABC bằng 100dm và chu vi tam giác A’B’C’ là 60dm.
Đúng 0
Bình luận (0)
Cho
Δ
A
B
C
∽
Δ
A
B
C
theo tỉ số đồng dạng 2. Gọi AM và AM lần lượt là các đường trung tuyến của tam giác này. Khi đó tỉ số
A
M
A
M
bằng A. 2 B.
1
2
C.
1...
Đọc tiếp
Cho Δ A B C ∽ Δ A ' B ' C ' theo tỉ số đồng dạng 2. Gọi AM và A'M' lần lượt là các đường trung tuyến của tam giác này. Khi đó tỉ số A M A ' M ' bằng
A. 2
B. 1 2
C. 1 4
D. 4
ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng
k
1
;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng
k
2
. ΔABC đồng dạng với Δ GHK theo tỉ số : A.
k
1
/
k
2
B.
k
1
+
k
2
C.
k
1
-
k
2...
Đọc tiếp
ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng k 1 ;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng k 2 . ΔABC đồng dạng với Δ GHK theo tỉ số :
A. k 1 / k 2
B. k 1 + k 2
C. k 1 - k 2
D. k 1 . k 2
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....
Cho ΔABC đồng dạng với ΔABC. Biết
A
B
A
B
2
5
và hiệu số chu vi của ΔA’B’C’và chu vi của ΔABC là 30. Phát biểu nào đúng A.
C
Δ
A
B
C
20
;
C
Δ
A...
Đọc tiếp
Cho ΔABC đồng dạng với ΔA'B'C'. Biết A B A ' B ' = 2 5 và hiệu số chu vi của ΔA’B’C’và chu vi của ΔABC là 30. Phát biểu nào đúng
A. C Δ A B C = 20 ; C Δ A ’ B ’ C ’ = 50
B. C Δ A B C = 50 ; C Δ A ’ B ’ C ’ = 20
C. C Δ A B C = 45 ; C Δ A ’ B ’ C ’ = 75
D. Cả ba đều sai
Cho ΔABC và ΔMNP đồng dạng với nhau theo tỉ số đồng dạng k = 3/2 . Chu vi tam giác ABC bằng 36cm. Chu vi tam giác MNP là:
A. 24cm
B. 54cm
C. 18cm
D. 12cm
cho ΔABC đồng dạng ΔHIK theo tỉ số đồng dạng k=7/3. Tính chu vi mỗi tam giác biết hiệu chu vi 2 tam giác là 48cm
Chu vi tam giác ABC:
\(48:\left(7-3\right).7=84\left(cm\right)\)
Chu vi tam giác HIK:
\(48:\left(7-3\right).3=36\left(cm\right)\)
Đúng 0
Bình luận (0)
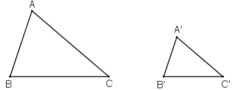
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35.
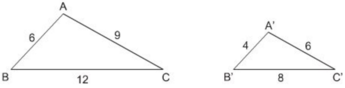
Hình 35
a) ΔABC và ΔA'B'C' có đồng dạng với nhau không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó.
a) Ta có:
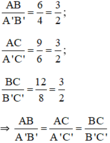
⇒ ΔABC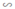 
ΔA’B’C’ (c.c.c).
b) Ta có:
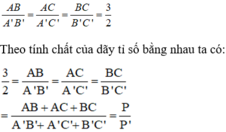
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là 3/2.
Đúng 0
Bình luận (0)
cho ΔABC có điểm M là trung điểm cạnh AC. Trên BM lấy điểm D sao cho DM=2.BM. Tia AD cắt BC tại K, cắt Bx tại E (Bx // AC)
a) tính tỉ số BE/AM
b) ΔBKE đồng dạng ΔCKA theo tỉ số đồng dạng là 1/4
c) tính tỉ số diện tích của ΔABK và ΔABC
