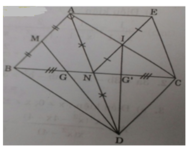
Cho hình chữ nhật ABCD có AB=3AD . Gọi M, N lần lượt là trung điểm của AB và CD, E là điểm đối xứng với N qua M, I là giao điểm của đường thẳng DM và EB.
a) C/m tứ giác AEBN là hình thoi.
b) Tứ giác AEID là hình gì? Vì sao?
c) Biết AB=6cm. Tính diện tích đa giác AEBCD.
HELP ME!!!!