cho tam giác ABC. vẽ các đường tròn (B;BA) và (C;A) chúng cắt nhau tại D (khác A). chứng minh rằng BC là tia phân giác của góc ABD

Những câu hỏi liên quan
Vẽ đường tròn nội tiếp tam giác:
Cho Trước tam giác ABC. Dùng các công cụ đường phân giác, đường vuông góc và đường tròn vẽ đường tròn nội tiếp tam giác ABC.
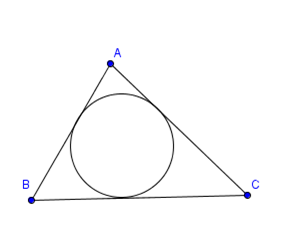
Đường tròn nội tiếp tam giác là là đường tròn tiếp xúc với 3 cạnh của tam giác.
Các bước vẽ đường tròn nội tiếp tam giác:
Vẽ tam giác ABC

Vẽ O là giao điểm 2 đường phân giác
Vẽ O là giao điểm 2 đường phân giác
 vẽ OM⊥AB→OMOM⊥AB→OM là bán kính
vẽ OM⊥AB→OMOM⊥AB→OM là bán kính

Vẽ đường tròn tâm O qua M
Vẽ đường tròn tâm O qua M


Vẽ O là giao điểm 2 đường phân giác
Vẽ O là giao điểm 2 đường phân giác
 vẽ OM⊥AB→OMOM⊥AB→OM là bán kính
vẽ OM⊥AB→OMOM⊥AB→OM là bán kính

Vẽ đường tròn tâm O qua M
Vẽ đường tròn tâm O qua M

Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn( AB AC) nội tiếp đường tròn(0;R) . Các đường cao AD , BE của tam giác ABC cắt nhau tại H .Vẽ đường kính AF của đường tròn ( O) .Gọi M là giao điểm của AD và đường tròn (O) (M khác A )
a )chứng minh rằng tứ giác BHCF là hình bình hành
b ) Chứng minh rằng BC là đường trung trực của đoạn thẳng HM
c) tứ giác BCFM m là hình gì? vì sao?
d) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và HG 2GO
Đọc tiếp
Cho tam giác ABC nhọn( AB < AC) nội tiếp đường tròn(0;R) . Các đường cao AD , BE của tam giác ABC cắt nhau tại H .Vẽ đường kính AF của đường tròn ( O) .Gọi M là giao điểm của AD và đường tròn (O) (M khác A ) a )chứng minh rằng tứ giác BHCF là hình bình hành b ) Chứng minh rằng BC là đường trung trực của đoạn thẳng HM c) tứ giác BCFM m là hình gì? vì sao? d) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và HG =2GO
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
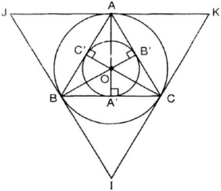
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
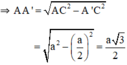
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
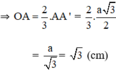
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 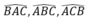
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
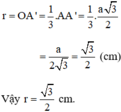
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
Đúng 0
Bình luận (2)
a/ Vẽ tam giác ABC, biết BC = 4 cm ; AB =2 cm ; AC= 3 cm
b/ Vẽ tiếp đường tròn C; 2cm, đường tròn này cắt cạnh AC tại M, cắt cạnh BC tại N, vẽ các đoạn thăng AN, MN. Hãy cho biết trên hình vẽ có bao nhiêu tam giác Gọi tên các tam giác ấy.
Bai1: Cho tam giác ABC nội tiếp đường tròn tâm O bán kính R. Các đỉnh B, C cố định còn A chạy trên đường tròn đó. Tìm tập hợp các trọng tâm G của tam giác ABC khi A di độngCho tam giác ABC nội tiếp đường tròn tâm O bán kính R. các bạn giúp mih` giải và vẽ hình bài này nhé help me đang cần gấp
giúp tôi với!!!!!! CÂU C
Cho điểm A nằm ngoài đường tròn (O;R) sao cho OA = 2R. Vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). a) Tam giác ABC là tam giác gì? Vì sao. b) Tính diện tích tam giác ABC theo R. b) Trên các đoạn thẳng AB và AC theo thứ tự lấy các điểm D và E sao cho góc DOE bằng 60 độ. Chứng minh DE là tiếp tuyến của đường tròn (O;R)
cho tam giác ABC vẽ đường tròn đường kính BC . vẽ đường cao AK của tam giác từ A vẽ tiếp tuyến AM,ĂN với tròn đường tròn (O). MN cắt AK tại H. chứng minh H là trưc tâm tam giác ABC
cho tam giác abc có ab=3cm, ac=4cm, bc=5cm. kẻ ah vuông góc với bc( h thuộc bc). a/ tam giác abc là tam giác gì? vì sao. b/ tính ah, góc b và c. c/ vẽ đường tròn( b, bh) và đường tròn ( c, ch). từ điểm a lần lượt vẽ tiếp tuyến am và an của đường tròn( b) và (c). tính góc mhn
a. \(BC^2=AB^2+AC^2\) nên ABC vuông tại A
b. Hệ thức lượng: \(AH=\dfrac{AB\cdot AC}{BC}=2,4\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx37^0\)
Đúng 3
Bình luận (0)
a) Vẽ tam giác đều ABC cạnh a = 3 cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O ; R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 0
Bình luận (0)

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 1
Bình luận (0)
Vẽ đoạn thẳng BC 3,5 cm. vẽ một điểm A sao cho AB 3cm,AC 2, 5 cm. Vẽ tam giác ABC. Đo các góc của tam giác ABCgiải:Cách vẽ tam giác ABC như sau:- Vẽ đoạn thẳng BC 3,5 cm- Trên cùng một nửa mặt phẳng bờ là đường thẳng BC:+ Vẽ cung tròn tâm B bán kính 3cm+ Vẽ cung tròn tâm C ..............................- Hai cung tròn tâm B. tâm C cắt nhau tại điểm ............- vẽ các đoạn thẳng .............. ta được tam giác ..............Dùng thước đo góc, đo các góc của tam giác ABC, ta đượcgóc BAC ......,...
Đọc tiếp
Vẽ đoạn thẳng BC= 3,5 cm. vẽ một điểm A sao cho AB = 3cm,AC= 2, 5 cm. Vẽ tam giác ABC. Đo các góc của tam giác ABC
giải:
Cách vẽ tam giác ABC như sau:
- Vẽ đoạn thẳng BC= 3,5 cm
- Trên cùng một nửa mặt phẳng bờ là đường thẳng BC:
+ Vẽ cung tròn tâm B bán kính 3cm
+ Vẽ cung tròn tâm C ..............................
- Hai cung tròn tâm B. tâm C cắt nhau tại điểm ............
- vẽ các đoạn thẳng .............. ta được tam giác ..............
Dùng thước đo góc, đo các góc của tam giác ABC, ta được
góc BAC= ......, góc ABC= ......, góc ACB=.........
+ Vẽ cung tròn tâm C bán kính 2,5cm
- Hai cung tròn tâm B. tâm C cắt nhau tại điểm A
- Vẽ các đoạn thẳng AB, AC, BC ta được tam giác ABC
góc BAC= , góc ABC= , góc ACB=
đợi chút
Đúng 0
Bình luận (0)



















