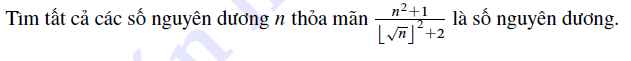
Làm hộ em bài này với ạ
P/s: [\(\sqrt{n}\)]\(^2\) là (phần nguyên của \(\sqrt{n}\))\(^2\)
Bài 1: Tìm số nguyên a lớn nhất sao cho số \(T=4^{27}+4^{1016}+4^a\) là số chính phương
Bài 2: Cho số tự nhiên \(N=2003^{2004}\). Viết N thành tổng của k số tự nhiên nào đó \(n_1,n_2,...,n_k.\)\(S=n_1^3+n_2^3+...+n_k^3.\)Tìm số dư của phép chia S cho 6.
Bài 3: CMR: \(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{n}}>2\left(\sqrt{n+1}-1\right)\)
Với n là số nguyên dương
Giúp em bài này với!!!
Chứng minh với mọi số n nguyên dương
\(\sqrt{1^3+2^3+..+n^3}=1+2+..+n.\)
chứng minh bằng phương pháp quy nap nhá bạn
Viết lại đẳng thức cần cm
\(1^3+2^3+..+n^3=\left(1+2+..+n\right)^2\)(*)
với n =1 thì \(1^3=1^2\)(ĐÚNG )
với n=2 thì \(1^3+2^3=9=3^2\)(ĐÚNG)
Giả sử (*) đúng với \(n=k\left(k\in N,k\ne0\right)\Leftrightarrow1^3+2^3+..+k^3=\left(1+2+..+k\right)^2\)
Ta đi chứng minh (*) đúng với n=k+1
Thạt vậy \(1^3+2^3+..+k^3+\left(k+1\right)^3=\left(1+..+k\right)^2+\left(k+1\right)^3\)
\(=\left(1+..+k\right)^2+\left(k+1\right)\left(k+1\right)^2=\left(1+..+k\right)^2+k\left(k+1\right)^2+\left(k+1\right)^2\)
\(=\left(1+..+k\right)^2+2\left(k+1\right)\left(1+..+k\right)+\left(k+1\right)^2=\left(1+..+k+k+1\right)^2\)(dpcm )
cho em hỏi đoạn này:
\(\left(1+..+k^2\right)+k\left(k+1\right)^2+\left(k+1\right)^2.\)sao lại bằng \(\left(1+..+k\right)^2+2\left(k+1\right)\left(1+..+k\right)+\left(k+1\right)^2..\)
chỗ \(k\left(k+1\right)^2\)biến đổi làm sao ạ?
giúp e câu này
Với mỗi số tự nhiên n, đặt Sn=(\(3-2\sqrt{2}\))n+(\(3+2\sqrt{2}\))n. CMR Sn là số nguyên với mọi số tự nhiên n và tìm số dư của S2016 khi chia cho 5
Cho biểu thức P = \(\sqrt{\frac{\left(x^3-3\right)^2+12x^3}{x^2}}+\sqrt{\left(x+2\right)^2-8x}\) . Tập các giá trị nguyên của x để biểu thức P có giá trị nguyên là S = {.....} (Viết các phần tử theo giá trị tăng dần, ngăn cách bởi dấu “;”)
( làm hộ tớ với ! )
So sánh:
\(\sqrt{n+2}-\sqrt{n+1}\) và \(\sqrt{n+1}-\sqrt{n}\)
(n là số nguyên dương)
Mọi người giúp mình với ạ. làm chi tiết nha. cảm ơn trước ạ :)
n là số nguyên dương
Bình phương hai vế, ta được:
\(\left(\sqrt{n+2}-\sqrt{n+1}\right)^2=n+2+n+1-2\sqrt{\left(n+2\right)\left(n+1\right)}\) \(=2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}\)
\(\left(\sqrt{n+1}-\sqrt{n}\right)^2=n+1+n-2\sqrt{n\left(n+1\right)}\) \(=2n+1-2\sqrt{n\left(n+1\right)}\)
Ta có: \(\left(n+2\right)\left(n+1\right)>n\left(n+1\right)\Rightarrow2\sqrt{\left(n+2\right)\left(n+1\right)}>2\sqrt{n\left(n+1\right)}\)
Mà 2n + 3 > 2n + 1
\(\Rightarrow2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}>2n+1-2\sqrt{n\left(n+1\right)}\)
=> ( √n+2 - √n+1)^2 > ( √n-1 - √n)^2
=> √n+2 - √n+1 > √n-1 - √n
P/s: Em làm còn sai nhiều, mong mọi người góp ý, đừng chọn sai cho em. Em cảm ơn
\(\sqrt{n+2}-\sqrt{n+1}\) và \(\sqrt{n+1}-\sqrt{n}\)
Bình phương mỗi số hạng, ta có:
\(\left(\sqrt{n+2}\right)^2-\left(\sqrt{n+1}\right)^2\) và \(\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2\)
\(n+2-n+1\) và \(n+1-n\) ( Vì \(n\ge0\))
\(3\) và \(1\)
\(\Rightarrow3>1\)
Vậy \(\sqrt{n+2}-\sqrt{n+1}>\sqrt{n+1}-\sqrt{n}\)
Giúp mk lm bài này nha mấy bạn: Cho f(n)=\(\frac{4n+\sqrt{4n^2-1}}{\sqrt{2n+1}+\sqrt{2n-1}}\) với n nguyên dương. Hãy tính giá trị của tổng: f(1)+f(2)+f(3)+..........+f(40)
MỌI NGƯỜI GIẢI HỘ MÌNH MẤY BÀI NÀY NHÉ:
Bài 1:
Cho a, b, c ∈ Z+. CMR nếu \(\sqrt{a}+\sqrt{b}+\sqrt{c}\)∈ Q thì a, b, c đồng thời là số chính phương.
Bài 2:
cho n ∈ Z+ không là số chính phương, \(\sqrt{n}\)là nghiệm của phương trình \(X^3+a.X^2+b.X+c=0\)(a,b,c ∈ Q)
tìm các nghiệm còn lại của phương trình.
Bài 3;
Tồn tại hay không số hữu tỉ a, b, c, d sao cho (\(\left(a+b.\sqrt{2}\right)^{1994}+\left(c+d.\sqrt{2}\right)^{1994}=5+4\sqrt{2}\)
Bài 4:
giải phương trình nghiệm nguyên \(\sqrt{x}+\sqrt{y}=\sqrt{1980}\)
Bài 5:
tìm x để \(\sqrt[3]{3+\sqrt{x}}+\sqrt[3]{3-\sqrt{x}}\)là số nguyên
Bài 6:
hãy biểu thị \(\sqrt[3]{2+\sqrt{5}}\)dưới dạng \(a+b.\sqrt{5}\)với a, b∈ Q
4. \(\sqrt{x}+\sqrt{y}=6\sqrt{55}\)
\(6\sqrt{55}\) là số vô tỉ, suy ra vế trái phải là các căn thức đồng dạng chứa \(\sqrt{55}\)
Đặt \(\sqrt{x}=a\sqrt{55};\sqrt{y}=b\sqrt{55}\) với \(a,b\in N\)
\(\Rightarrow a+b=6\)
Xét các TH:
a = 0 => b = 6
a = 1 => b = 5
a = 2 => b = 4
a = 3 => b = 3
a = 4 => b = 2
a = 5 => b = 1
a = 6 => b = 0
Từ đó dễ dàng tìm đc x, y
Các thánh ơi cứu em với, giải hộ em bài toán này với
Tìm n thuộc N để số n2 + 6n là số nguyên tố
n2 + 6n = n(n + 6) chia hết n
Mà n2 + 6n phải là số nguyên tố => n = 1
Thử lại: n(n + 6) = 7 nguyên tố
Vậy n = 1
Tìm phần nguyên của a, với \(a=\sqrt{2}+\sqrt[3]{\frac{3}{2}}+\sqrt[4]{\frac{4}{3}}+...+\sqrt[n+1]{\frac{n+1}{n}}\)
Ta có:
Áp dụng bất đẳng thức Cauchy cho k + 1 số ta có:
Lần lượt cho k = 1, 2, 3, ... rồi cộng lại ta được