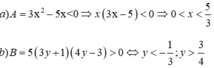sao hai cái y rk

help đi

\(B=3\left(2y+3\right)\left(3y-5\right)\)là sô âm 

\(\Rightarrow B< 0\)tức \(3\left(2y+3\right)\left(3y-5\right)< 0\)

để \(3\left(2y+3\right)\left(3y-5\right)< 0\)thì \(3;2y+3;3y-5\ne\)dấu

th1\(\hept{\begin{cases}3>0\\2y+3< 0\\3y-5>0\end{cases}\Leftrightarrow\hept{\begin{cases}3>0\\2y< -3\\3y>5\end{cases}}\Leftrightarrow\hept{\begin{cases}3>0\\y< \frac{-3}{2}\\y>\frac{5}{3}\end{cases}}\Rightarrow\frac{5}{3}< y< \frac{-3}{2}\left(l\right)}\)

th2\(\hept{\begin{cases}3>0\\2y+3>0\\3y-5,0\end{cases}\Leftrightarrow\hept{\begin{cases}3>0\\2y>-3\\3y< 5\end{cases}}\Leftrightarrow\hept{\begin{cases}3>0\\y>\frac{-3}{2}\\y< \frac{5}{3}\end{cases}}\Rightarrow\frac{-3}{2}< y< \frac{5}{3}\left(tm\right)}\)

=>.....

hình như đề sai

Bài 1:

a)   \(x^2+5x=x\left(x+5\right)< 0\)  (1)

Nhận thấy:   \(x< x+5\)

nên từ (1)   \(\Rightarrow\)  \(\hept{\begin{cases}x< 0\\x+5>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x< 0\\x>-5\end{cases}}\)\(\Leftrightarrow\)\(-5< x< 0\)

Vậy.....

b)   \(3\left(2x+3\right)\left(3x-5\right)< 0\)

TH1:   \(\hept{\begin{cases}2x+3>0\\3x-5< 0\end{cases}}\)\(\Leftrightarrow\)  \(\hept{\begin{cases}x>-\frac{3}{2}\\x< \frac{5}{3}\end{cases}}\)\(\Leftrightarrow\)\(-\frac{3}{2}< x< \frac{5}{3}\)

TH2:  \(\hept{\begin{cases}2x+3< 0\\3x-5>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x< -\frac{3}{2}\\x>\frac{5}{3}\end{cases}}\)  vô lí

Vậy   \(-\frac{3}{2}< x< \frac{5}{3}\)

Bài 2:

a)  \(2y^2-4y=2y\left(y-2\right)>0\)

TH1:   \(\hept{\begin{cases}y>0\\y-2>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y>0\\y>2\end{cases}}\)\(\Leftrightarrow\)\(y>2\)

TH2:  \(\hept{\begin{cases}y< 0\\y-2< 0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y< 0\\y< 2\end{cases}}\)\(\Leftrightarrow\)\(y< 0\)

Vậy  \(\orbr{\begin{cases}y< 0\\y>2\end{cases}}\)

b)  \(5\left(3y+1\right)\left(4y-3\right)>0\)

TH1:  \(\hept{\begin{cases}3y+1>0\\4y-3>0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y>-\frac{1}{3}\\y>\frac{3}{4}\end{cases}}\)\(\Leftrightarrow\)\(y>\frac{3}{4}\)

TH2:  \(\hept{\begin{cases}3y+1< 0\\4y-3< 0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}y< -\frac{1}{3}\\y< \frac{3}{4}\end{cases}}\)\(\Leftrightarrow\)\(y< -\frac{1}{3}\)

Vậy   \(\orbr{\begin{cases}y>\frac{3}{4}\\y< -\frac{1}{3}\end{cases}}\)

nhận giá trị âm tức là giá trị của biểu thức nhỏ hơn 0 và ngược lại!

a) \(15-3x< 0\)

\(\Leftrightarrow-3x< -15\)

\(\Leftrightarrow3x>5\)

b) \(27x+9< 0\)

\(\Leftrightarrow27x< -9\)

\(\Leftrightarrow x< -\frac{1}{3}\)

c) \(2y^2-4x< 0\)

\(\Leftrightarrow2\cdot\left(y^2-2x\right)< 0\)

\(\Leftrightarrow y^2-2x< 0\)

......

Để D dương

TH1:

\(\hept{\begin{cases}3x+1>0\\4x-3< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{-1}{3}\\x< \frac{3}{4}\end{cases}\Leftrightarrow}\frac{-1}{3}< x< \frac{3}{4}}\)(chọn)

TH2:

\(\hept{\begin{cases}3x+1< 0\\4x-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}x< \frac{-1}{3}\\x>\frac{3}{4}\end{cases}}}\)( loại )

vậy \(\frac{-1}{3}< x< \frac{4}{3}\)để biểu thức D nhận giá trị dương

\(D=5\left(3x+1\right)\left(4x-3\right)\)

th1 : \(\hept{\begin{cases}3x+1>0\\4x-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>-\frac{1}{3}\\x>\frac{3}{4}\end{cases}\Leftrightarrow}x>\frac{3}{4}}\)

th2 : \(\hept{\begin{cases}3x+1< 0\\4x-3< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< -\frac{1}{3}\\x< \frac{3}{4}\end{cases}\Leftrightarrow}x< -\frac{1}{3}}\)

\(\Rightarrow\hept{\begin{cases}x>\frac{3}{4}\\x< -\frac{1}{3}\end{cases}}\)