Cho tam giác ABC. Vẽ tia AD là tia đối của tia AB. Trên nửa mặt phẳng bờ Ab có chứa điểm C, vẽ tia AM là tia phân giác của góc CAD. Biết AM// BC. Chứng tỏ rằng góc B = góc C
Những câu hỏi liên quan
Cho tam giác ABC. Vẽ tia AD là tia đối của tia AB. Trên nửa mặt phẳng bờ AB có chứa điểm C, vẽ tia AM là tia phân giác của góc CAD. Biết AM//BC. Chứng tỏ rằng góc B = góc C
cho tam giác abc vẽ tia ad là tia đối của tia ab trên nửa mặt phẳng bờ ab c vẽ tia phân giác am của góc cad. biết am song song bc và goc b thuộc góc c
cho tam giac ABC có góc B=góc C.Vẽ tia AD là tia đối của tia AB. Trên nửa mặt phẳng bờ AB chứa điiểm C, vẽ tia AM sao cho AM song song với BC. chứng minh AM là tia phân giác của góc CAD
giúp mình với
Cho tam giác ABC vẽ AD là tia phân giác goc BAC , ( Điểm D thuộc BC ) vẽ tia AX là tia đối của tia AC . Vẽ tia BI trên nửa mặt phẳng bờ AB không chứa C sao cho góc ABI=CAD. Chứng tỏ IBC=ADC
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD = AB. Trên nửa mặt phẳng không chứa B có bờ là AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE = AC. Chứng minh rằng: a) AM=DE/2 b) AM⊥ DE
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD = AB. Trên nửa mặt phẳng không chứa B có bờ là AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE = AC. Chứng minh rằng: a) AM=\frac{DE}{2} b) AM \perp \ DE
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE=AC. Chứng minh rằng:
a) AM=DE/2
b)AM vuông góc DE
Câu này của nâng cao lớp 7 bạn ạ
Đúng 0
Bình luận (0)
a, Để chứng tỏ DE = 2AM,ta tạo ra đoạn thẳng gấp đôi AM bằng cách lấy K trên tia đối của tia MA sao cho MK = MA,ta sẽ chứng minh AK = DE
Dễ thấy AC = BK, AC // BK . Xét \(\Delta ABK\)và \(\Delta DAE\), ta có :
AB = AD gt
BK = AE cùng bằng AC
\(\widehat{ABK}=\widehat{DAE}\)cùng bù với góc BAC
Do đó \(\Delta ABK=\Delta DAE(c.g.c)\)
\(\Rightarrow AK=DE\)hai cạnh tương ứng
Vậy AM = DE/2
b, Gọi H là giao điểm của MA và DE.Ta có \(\widehat{BAK}+\widehat{DAH}=90^0\)nên \(\widehat{D}+\widehat{DAH}=90^0\), do đó góc AHD = 900
Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB chứa C, vẽ tia Ax vuông góc AB;trên nửa mặt phẳng bờ AC chứa B, vẽ tia Ấy vuông góc AC. Lấy điểm D thuộc tia Ax sao cho AD=AB, điểm E thuộc tia Ấy sao cho AE=AC. Gọi M là Trung điểm BC. Chứng minh: AM vuông góc với DE, AM=1/2DE
Bài 10: Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD = AB. Trên nửa mặt phẳng không chứa B có bờ là AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE = AC. Chứng minh rằng:
a) AM=1/2DE
b,AM vuong goc DE
Cho tam giác ABC,
A
^
70
°
;
B
^
55
°
. Trên tia đối của tia AB lấy điểm M. Vẽ tia Mx trên nửa mặt phẳng bờ MB không chứa C sao cho
B
M
x
^
55
°
. Vẽ tia Ay là tia phân giác của góc CAM. Chứng tỏ rằng Mx // BC và Ay // BC
Đọc tiếp
Cho tam giác ABC, A ^ = 70 ° ; B ^ = 55 ° . Trên tia đối của tia AB lấy điểm M. Vẽ tia Mx trên nửa mặt phẳng bờ MB không chứa C sao cho B M x ^ = 55 ° . Vẽ tia Ay là tia phân giác của góc CAM. Chứng tỏ rằng Mx // BC và Ay // BC
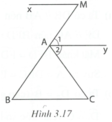
Ta có B M x ^ = B ^ = 55 ° . Suy ra M x / / B C vì có cặp góc so le trong bằng nhau.
Ta có C A M ^ + C A B ^ = 180 ° (hai góc kề bù)
C A M ^ = 180 ° − 70 ° = 110 ° .
Tia Ay là tia phân giác của góc CAM
⇒ A 1 ^ = A 2 ^ = 55 ° , do đó A 1 ^ = B ^ = 55 ° .
Suy ra A y / / B C vì có cặp góc đồng vị bằng nhau
Đúng 0
Bình luận (0)