Cho A,B,C thẳng hàng , B nằm giữa A và C. Dựng về phía đường thẳng AC các \(\Delta ABE\) và BCF đều . M,N là trung điểm của AF và EC. Cm tam giác BMN đều

Những câu hỏi liên quan
Trên đoạn thẳng AB ta lấy một điểm C nằm giữa A và B . Dựng các tam giác đều ACE và BCF sao cho E, F nằm cùng phía đối với đường thẳng AB.
a) So sánh độ dài hai đoạn thẳng AF và BE
b) Gọi M và N lần lượt là trung điểm các đoạn thẳng AF và BE. Khi đó tam giác AMN có đặc điểm gì?
Cho 3 điểm A, B, C thẳng hàng và B nằm giữa A và C. Dựng về một phía của đường thẳng AC các tam giác đều ABE và BCF. Tính góc giữa hai đường thẳng AF và CE. giải thích tại sao?
Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:
A. tam giác thường
B. tam giác vuông đỉnh B
C. tam giác cân đỉnh B
D. tam giác đều
Xét phép quay tâm B góc quay -600 biến A thành D, biến E thành C suy ra phép quay này biến đoạn thẳng AE thành đoạn thẳng DC, suy ra nó biến trung điểm F của AE thành trung điểm G của DC, suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600. Vậy tam giác BFG là tam giác đều.
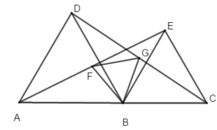
Đáp án D
Đúng 0
Bình luận (0)
Cho tam giác ABC . Về phía ngoài của tam giác ABC dựng các tam giác đều ABD , ACE , BCF .
a/ C/m BE =CD= AF
b/ I J, lần lượt là trung điểm của các đoạn thẳng BE , CD . Chứng minh tam giác AIJ đều
cho tam giác ABD là tam giác đều. Về phía ngoài tam giác ABD các tam giác vuông cân tại A là tam giác ABC và tam giác AC
a,cm: tam giác ACD = tam giác ABE
b,Gọi AM là tia phân giác của góc BAD; N là trung điểm của CE.CM Ạ,N,M thẳng hàng
các bạn hãy trả lời nhanh câu hỏi ở bên trên cho mình
Đúng 0
Bình luận (0)
cho tam giác ABC có A= 60 0 . Dựng ra phía ngoài các tam giác đều ABM ,ACN . a/ C/m : ba điểm M,A,N thẳng hàng . b/ C/m : BN = CM . c/Gọi O là giao điểm của BN và CM . Tính BOC ?
a)Góc MAN =60+60+60 =180 => M,A,N thẳng hàng
b)Xét tam giác ABN và AMC : có AB=AM ; góc NAB = góc CAM =120; AN = AC
=> ABN =AMC ( c-g-c)
=> BN =MC cạnh tương ứng
c)Gọi K là giao điểm AB và MC
Xét 2 tam giác KAM và KOB
theo b =>góc M = góc B
H1 = H2 đối đỉnh
=> A=O =60
Mà O+ BOC =180=> BOC =180 -60 =120
Đúng 0
Bình luận (1)
cho đường thẳng AB. Điểm C nằm giữa A và B. trên cùng mặt phẳng bờ AB vẽ 2 tam giác đều ACD và BCF. gọi M và N lần lượt là trung điểm của AE và BD. chứng minh AE=BD
Bài 1: ChoDelta ABCleft(AB ACright).Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C và BDCE. Gọi M,N,I lần lượt là trung điểm của BC, DE, BE.a) CMR: Delta MINcânb) Đường thẳng MN cắt đường thẳng AB ở P, cắt đường thẳng AC ở Q. CM tam giác APQ cânc) Kẻ phân giác AF của tam giác ABC. CM MN//AFGiúp mk nha m.n mk đang cần gấp lắm ai làm nhanh mk tk
Đọc tiếp
Bài 1: \(Cho\Delta ABC\left(AB< AC\right)\).Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C và BD=CE. Gọi M,N,I lần lượt là trung điểm của BC, DE, BE.
a) CMR: \(\Delta MIN\)cân
b) Đường thẳng MN cắt đường thẳng AB ở P, cắt đường thẳng AC ở Q. CM tam giác APQ cân
c) Kẻ phân giác AF của tam giác ABC. CM MN\(//\)AF
Giúp mk nha m.n mk đang cần gấp lắm ai làm nhanh mk tk
Rất Sorry bạn nha.Mik mới nghĩ ra câu a,b thôi,còn câu c thì mik cần thời gian:(

Bạn tự chứng minh bổ đề đường trung bình nha.
a.
Do N là trung điểm của DE;I là trung điểm của BE nên NI là đường trung bình của tam giác BDE nên:
\(IN=\frac{1}{2}BD\left(1\right)\)
Mặt khác:M là trung điểm của BC,I là trung điểm của BE nên MI là đường trung bình của tam giác BEC nên:
\(IM=\frac{1}{2}EC\left(2\right)\)
Mà \(BD=EC\) nên từ (1);(2) suy ra \(IN=MI\Rightarrow\Delta IMN\) cân tại I.
b.
Do IN là đường trung bình nên \(IN//AB\Rightarrow\widehat{APQ}=\widehat{INM}\left(3\right)\)
Do IM là đường trung bình nên \(IM//EC\Rightarrow\widehat{AQP}=\widehat{IMN}\left(4\right)\)
Từ (3);(4) suy ra \(\widehat{APQ}=\widehat{AQP}\Rightarrow\Delta APQ\) cân tại A.
Đúng 1
Bình luận (0)
Cho ABC (AB < AC). Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C và BD = CE. Gọi M, N, I lần lượt là trung điểm của BC, DE, BE.. a)Đường thẳng MN cắt đường thẳng AB ởP, cắt đường thẳng AC ởQ. Chứng minh tam giác APQ cân.b )Kẻphân giác AF của tam giác ABC. Chứng minh MN // AF.













