Tính bán kính (R) ngtử gần đúng của Mg ở 20*C biết ở nhiệt độ đó Mg có khối lượng riêng (D) là 1,74g/cm3 . Biết Mg có mạng tinh thể lục phương có độ đặt khít là 74,05%

Những câu hỏi liên quan
Bán kính nguyên tử gần đúng của nguyên tử R ở 2000C là 1,965.10-8 cm biết tại nhiệt độ đó khối lượng riêng của R bằng 1,55 g/cm3. Giả thiết trong tinh thể các nguyên tử R có hình cầu, có độ đặc khít là 74%. R là nguyên tố A. Mg B. Cu C. Al D. Fe
Đọc tiếp
Bán kính nguyên tử gần đúng của nguyên tử R ở 2000C là 1,965.10-8 cm biết tại nhiệt độ đó khối lượng riêng của R bằng 1,55 g/cm3. Giả thiết trong tinh thể các nguyên tử R có hình cầu, có độ đặc khít là 74%. R là nguyên tố
A. Mg
B. Cu
C. Al
D. Fe
Bán kính nguyên tử gần đúng của nguyên tử R ở 2000C là 1,965.10-8 cm biết tại nhiệt độ đó khối lượng riêng của R bằng 1,55 g/cm3. Giả thiết trong tinh thể các nguyên tử R có hình cầu, có độ đặc khít là 74%. R là nguyên tố A. Mg B. Cu C. Al D. Fe
Đọc tiếp
Bán kính nguyên tử gần đúng của nguyên tử R ở 2000C là 1,965.10-8 cm biết tại nhiệt độ đó khối lượng riêng của R bằng 1,55 g/cm3. Giả thiết trong tinh thể các nguyên tử R có hình cầu, có độ đặc khít là 74%. R là nguyên tố
A. Mg
B. Cu
C. Al
D. Fe
Đáp án D
Áp dụng công thức
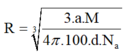 ta có:
ta có:
 R là Ca.
R là Ca.
Đúng 0
Bình luận (0)
Bán kính nguyên tử gần đúng của nguyên tử R ở 25 độ C là 1,965.10-8cm. Biết tại nhiệt độ đó khối lượng riêng của R kim loại là 1,55 g/cm3. Giả thiết rằng, trong tinh thể R các nguyên tử là những hình cầu chiếm 74% thể tích tinh thể, phần còn lại là rỗng. R là chất gì?
Mong mọi ng giúp e
Cho biết khối lượng nguyên tử của Mg là 24,305 và khối lượng riêng của magie kim loại là 1,74 g/cm3. Giả thiết các nguyên tử Mg là hình cầu nội tiếp trong các hình lập phương. Bán kính gần đúng của nguyên tử Mg là (đơn vị nm): A. 0,15 B. 0,166 C. 0,142 D. 0,25
Đọc tiếp
Cho biết khối lượng nguyên tử của Mg là 24,305 và khối lượng riêng của magie kim loại là 1,74 g/cm3. Giả thiết các nguyên tử Mg là hình cầu nội tiếp trong các hình lập phương. Bán kính gần đúng của nguyên tử Mg là (đơn vị nm):
A. 0,15
B. 0,166
C. 0,142
D. 0,25
Giả sử có 1 mol nguyên tử Mg thì chứa 6,02. 1023 nguyên tử Mg
Thể tích của 1 mol nguyên tử Mg là V=
24
,
305
1
,
74
Ta có Vnguyên tử =
V
6
,
02
.
10
23
Gọi cạnh của hình lập phương là a cm. Vì các nguyên tử Mg là hình cầu nội tiếp trong các hình lập phương nên bán kính của nguyên tử Mg là r= 0,5a
Ta có thể tích của hình lập phương là a3 = (2r)3=
V
6
,
02
.
10
23
→ 8r3 =
24
,
305
1
,
74
.
6
,
03
.
10
23
→ r = 1,42. 10-8 cm = 0,142 nm.
Đáp án C.
Đúng 0
Bình luận (0)
Tính bán kính gần đúng của Ag ở 20oC biết ở nhiệt đọ đó khối lượng riêng của Ag là 19,23g/cm3. Giả thiết trong tinh thể Ag là hình cầu chiếm 75% thể tích còn lại là khe trống. Biết mAg= 196,97g.
tinh thể Ag chiếm 75 % thể tích => khối lượng riêng của nguyên tử Ag = 19,23/0,75= 25,64 (g/cm3)
áp dụng ct : V = \(\frac{4\sqcap r^3}{3}\) => r = ³√[(196,97.1,66.10^-24/25,64) /(4π/3)] cm
Đúng 0
Bình luận (0)
Ở điều kiện thường, crom có cấu trúc mạng lập phương tâm khối trong đó thể tích của các nguyên tử chiếm 68% thể tích tinh thể. Khối lượng riêng của crom là 7,2 gam/cm3. Nếu coi nguyên Cr có dạng hình cầu thì bán kính gần đúng của nó là: A. 0,125nm B. 0,155nm C. 0,134nm D. 0,165nm
Đọc tiếp
Ở điều kiện thường, crom có cấu trúc mạng lập phương tâm khối trong đó thể tích của các nguyên tử chiếm 68% thể tích tinh thể. Khối lượng riêng của crom là 7,2 gam/cm3. Nếu coi nguyên Cr có dạng hình cầu thì bán kính gần đúng của nó là:
A. 0,125nm
B. 0,155nm
C. 0,134nm
D. 0,165nm
Đáp án A
xét 1 mol nguyên tủ Crom: có số nguyên tử Crom là 6.022. 10 23 nguyên tử và khối lượng là 52.
Thể tích của 1 mol nguyên tử Crom là:
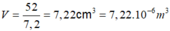
Thể tích thực của 1 nguyên tử Crom là:
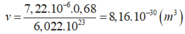
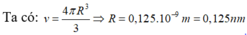
Đúng 0
Bình luận (0)
Ở điều kiện thường Crom có cấu trúc mạng lập phương tâm khối trong đó thể tích các nguyên tử chiếm 68% thể tích tinh thể. Khối lượng riêng của Cr là 7,2 g/cm3. Nếu coi nguyên tử Cr có dạng hình cầu thì bán kính gần đúng của nó là A. 0,155 nm B. 0,125 nm C. 0,134 nm D. 0,165 nm
Đọc tiếp
Ở điều kiện thường Crom có cấu trúc mạng lập phương tâm khối trong đó thể tích các nguyên tử chiếm 68% thể tích tinh thể. Khối lượng riêng của Cr là 7,2 g/cm3. Nếu coi nguyên tử Cr có dạng hình cầu thì bán kính gần đúng của nó là
A. 0,155 nm
B. 0,125 nm
C. 0,134 nm
D. 0,165 nm
Khối lượng riêng của Cr là 7,2 g/cm3;
nghĩa là 7,2 gam Cr ↔ 7,2 ÷ 52 × 6,023 × 1023 hạt nguyên tử Cr chiếm thể tích là 1cm3 = 10-6 m3.
Lại để ý: mỗi nguyên tử chỉ chiếm 68% thể tích tinh thể (còn lại là rỗng),
nghĩa là thể tích thực của mỗi nguyên tử Crom là:
V1 nguyên tử = 10-6 × 0,68 ÷ (7,2 ÷ 52 × 6,023 × 1023)) = 4 ÷ 3πr3.
Bấm fx CASIO có ngay r = 1,25 × 10-10 m = 0,125 nm.
ta chọn đáp án B.
Đúng 0
Bình luận (0)
Bán kính nguyên tử gần đúng của nguyên tử R ở 250C là 1,965.10-8cm. Biết tại nhiệt độ đó khối lượng riêng
của R kim loại là 1,55 g/cm3. Giả thiết rằng, trong tinh thể R các nguyên tử là những hình cầu chiếm 74% thể tích tinh
thể, phần còn lại là rỗng. R là chất gì?
Thể tích của nguyên tố R: \(V_1=\dfrac{M}{d}\)
Giả thiết rằng, trong tinh thể R các nguyên tử là những hình cầu chiếm 74%
=> Thể tích của tất cả nguyên tử là:\(V_2=V_1.0,74\)
Thể tích của từng nguyên tử là: \(V_3=\dfrac{V_2}{6,023.10^{23}}\)
Mặt khác: \(V_3=\dfrac{4}{3}.pi.R^3=3,178.10^{-23}cm^3\)
\(\Rightarrow M=\dfrac{3,178.10^{-23}.6,023.10^{23}.1,55}{0,74}=40\)
=> R là Ca
Đúng 3
Bình luận (0)
Một kim loại M kết tinh theo mạng lập phương tâm khối có cạnh hình lập phương là 5,32 Angstrom, độ đặc khít 68%, khối lượng riêng của M ở trạng thái tinh thể là 0,86 g/cm3. M là A. K. B. Li. C. Na. D. Rb.
Đọc tiếp
Một kim loại M kết tinh theo mạng lập phương tâm khối có cạnh hình lập phương là 5,32 Angstrom, độ đặc khít 68%, khối lượng riêng của M ở trạng thái tinh thể là 0,86 g/cm3. M là
A. K.
B. Li.
C. Na.
D. Rb.
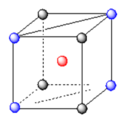
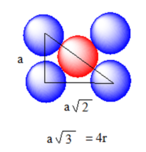
Vì M cấu tạo lập phương tâm khối nên trong 1 ô cơ sở có 2 đơn vị nguyên tử nằm vừa đủ trên đường chéo chính
Độ dài của cạnh lập phương là a → độ dài của đường chéo chính là
3
a = 4r → r =
3
.
5
,
32
.
10
-
8
4
Giả sử 1 mol nguyên tử M.
Thể tích của 1 nguyên tử M là
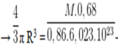
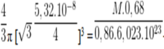
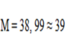
Vậy M là K.
Đáp án A.
Đúng 0
Bình luận (0)









