Giải

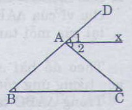
$\widehat{CAD}$= $\hat{B}$+ $\hat{C}$(góc ngoài của tam giác ABC)

= 40⁰+ 40⁰ = 80⁰

$\widehat{A_2}=\frac{1}{2}\widehat{CAD}=\frac{80}{2}=$40^0.

Hai góc so le trong bằng nhau nên Ax// Bc

Theo đề ta giải được : \(\widehat{A}=100^0\)

Gọi à là tia phân giác ngoài của góc A .

\(\Rightarrow\widehat{A_2}=\widehat{A_3}=\frac{\left(180^0-100^0\right)}{2}=\frac{80^0}{2}=40^0\)

\(\Rightarrow\widehat{A_2}=\widehat{C}\left(=40^0\right)\)

Mà góc A 1 và góc C là hai góc so le trong .

=> Ax // BC ( đpcm )

Gọi góc CAy là góc ngoài của tam giác ABC

Ta có Ax là tia p/g của góc CAy nên góc CAx=góc xAy=góc CAy:2=(góc C+góc B):2=(40 độ +40 độ):2=40 độ

=>Góc xAC=góc C(=40 độ)

Mà hai góc này ở vị trí so le trong

=>Ax//BC

Tam giác ABC có: góc B +góc C + góc BAC = 180^o => 40^o + 40^o + BAC = 180^o => góc BAC = 180^o - 80^o = 100^o

=> góc BAy = 180^o - BAC = 180^o - 100^o = 80^o (do BAy là góc ngoài tam giác )

=> góc xAB = yAB/2 = 80^o/2 = 40^o (do Ax là p/g của góc yAB)

=> góc xAB = ABC (= 40^o) Mà hai góc này ở vị trí SLT => Ax // BC

xin lỗi nha mình ko biết vẽ hình

cmsa;lcsacascsa

\(\widehat{BAC}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-80^o=100^o\)

\(\widehat{yAc}=180^o-100^o=80^o\)

Mà tia Ax là tia phân giạc góc ngoài của A

\(\Rightarrow\widehat{yAx}=\widehat{xAC}=\frac{\widehat{yAc}}{2}=\frac{80^o}{2}=40^o\)

Ở vị trí so le trong => Ax//BC

thanks

Tam giác ABC có: góc B +góc C + góc BAC = 180 o => 40 o + 40 o + BAC = 180 o => góc BAC = 180 o - 80 o = 100 o

=> góc BAy = 180 o - BAC = 180 o - 100 o = 80 o (do BAy là góc ngoài tam giác )

=> góc xAB = yAB/2 = 80 o/2 = 40 o (do Ax là p/g của góc yAB)

=> góc xAB = ABC (= 40 o) Mà hai góc này ở vị trí SLT => Ax // BC

thanhs