Một đa giác có 209 đường chéo. Hỏi đa giác có bao nhiêu cạnh

Những câu hỏi liên quan
Một Đa giác lồi có tất cả 170 đường chéo. Hỏi đa giác đó có bao nhiêu cạnh?
(Đa giác lồi n cạnh có n(n - 3) : 2 đường chéo)
theo bạn nói thì đa giác lồi có n(n-3) :2 đường chéo
Mà đa giác lồi này có 170 đường chéo
=> n(n-3):2 = 170
=> n(n-3) = 340
=> n(n-3) = 20.17
<=> n = 20
Vậy đa giác lồi này có 20 cạnh
Đúng 1
Bình luận (0)
Một đa giác có tất cả 170 đường chéo hỏi đa giác đó có bao nhiêu cạnh
Số đường chéo của một đa giác lồi có x cạnh là:
x * ( x - 3 ) / 2 = 170
<=> x2 - 3x - 340 = 0
<=> x = 20 (N)
n = -17 (L)
Đúng 2
Bình luận (0)
một đa giác có 20225077 đường chéo. hỏi đa giác đó có bao nhiêu cạnh
cho đa giác lồi có 20 cạnh hỏi có bao nhiêu tứ giác có 2 cạnh là cạnh của đa giác và 2 cạnh là đường chéo của đa giác
Một đa giác lồi có tất cả các đường chéo dài bằng nhau. Hỏi đa giác này có thể có bao nhiêu cạnh?.................................... giải dùm nhé mọi người,,,,,,,
Bài 1: Tìm số cạnh của một đa giác biết số đường chéo hơn số cạnh là 7.
Bài 2: Tổng tất cả các góc trong và một góc ngoài của một đa giác có số đo là 47058,5°. Hỏi đa giác đó có bao nhiêu cạnh?
Bài 3: Tổng số đo các góc của một đa giác n - cạnh trừ đi góc A của nó bằng 5700. Tính số cạnh của đa giác đó và A.
Bài 4: Một lục giác đều và một ngũ giác đều chung cạnh AD (như hình vẽ). Tính các góc của tam giác ABC: (Hình đây)
[Giúp mình với mng ơi, mình cần gấp. Mấy bài trên thuộc bài Đa giác, đa giá...
Đọc tiếp
Bài 1: Tìm số cạnh của một đa giác biết số đường chéo hơn số cạnh là 7.
Bài 2: Tổng tất cả các góc trong và một góc ngoài của một đa giác có số đo là 47058,5°. Hỏi đa giác đó có bao nhiêu cạnh?
Bài 3: Tổng số đo các góc của một đa giác n - cạnh trừ đi góc A của nó bằng 5700. Tính số cạnh của đa giác đó và A.
Bài 4: Một lục giác đều và một ngũ giác đều chung cạnh AD (như hình vẽ). Tính các góc của tam giác ABC: (Hình đây)
[Giúp mình với mng ơi, mình cần gấp. Mấy bài trên thuộc bài Đa giác, đa giác đều nha]
một đa giác có 2013020 đường chéo. hỏi đa giác có bao nhiêu canh
Trong một đa giác đều bảy cạnh, kẻ các đường chéo. Hỏi có bao nhiêu giao điểm của các đường chéo, trừ các đỉnh?
Mỗi giao điểmcủa hai đường chéoứng với một và chỉ một tập hợp gồm 4 điểmtừ tập hợp 7 đỉnh của đa giác. Vậy có 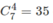 giao điểm.
giao điểm.
Đúng 0
Bình luận (0)
Cho đa giác n đỉnh (n>4)
a) Đếm số đường chéo của đa giác
b) Có bao nhiêu tam giác có đỉnh là đỉnh của đa giác
c) Có bao nhiêu tam giác có 2 cạnh là 2 cạnh của đa giác
d) Có bao nhiêu tam giác chỉ có 1 cạnh là cạnh của đa giác
e) Có bao nhiêu tam giác không có cạnh nào của đa giác
a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)
Đúng 2
Bình luận (0)















