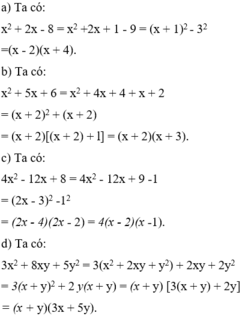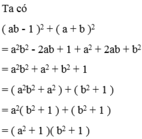Ta có:A= 3a+3b-a^2-ab

=>A= (3a-a^2)+(3b-ab)

=>A= a(3-a)+b(3-a)

=>A= (a+b)(3-a)

tớ mới học lớp 6

mk mới hk lớp 6 thui ak

d) (y3 + 8) + ( y2 – 4) =(y3 + 23) + ( y2 – 22)

= (y + 2)(y2 – 2y + 4) + (y + 2)( y – 2)

= (y + 2)(y2 – 2y + 4 + y – 2) = (y + 2)(y2 – y + 2)

\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)

\(4a^3-3a+1\)

\(=\left(4a^3-4a\right)+\left(a+1\right)\)

\(=4a\left(a^2-1\right)+\left(a+1\right)\)

\(=4a\left(a-1\right)\left(a+1\right)+\left(a+1\right)\)

\(=\left(a+1\right)\left(4a^2-4a+1\right)\)

\(=\left(a+1\right)\left(2a-1\right)^2\)

a) \(\left(a^2+b^2-5\right)^2-2\left(ab+2\right)^2\)

\(=\left(a^2+b^2-5\right)^2-\left(\sqrt{2}.ab+\sqrt{2}.2\right)^2\)

\(=\left(a^2+b^2-5-\sqrt{2}.ab-\sqrt{2}.2\right).\left(a^2+b^2-5+\sqrt{2}.ab+\sqrt{2}.2\right)\)

b) \(\left(4a^2-3a-18\right)^2-\left(4a^2+3a\right)^2\)

\(\left(4a^2-3a-18-4a^2-3a\right).\left(4a^2-3a-18+4a^2+3a\right)\)

\(=\left(-6a-18\right).\left(8a^2-18\right)\)

\(=\left(-6\right).\left(a+3\right).2.\left(4a^2-9\right)\)

\(=\left(-12\right).\left(a+3\right).\left(2a-3\right).\left(2a+3\right)\)

a) Xem lại đề

b) ( 4a² - 3a - 18 )² - ( 4a² + 3a )²

= [ ( 4a² - 3a - 18 ) - ( 4a² + 3a ) ][ ( 4a² - 3a - 18 )​ + ( 4a² + 3a ) ]

= ( 4a² - 3a - 18 - 4a² - 3a )( 4a² - 3a - 18 + 4a² + 3a )

= ( -6a - 18 )( 8a² - 18 )

= -6( a + 3 ).2( 4a² - 9 )

= -12( a + 3 )( 4a² - 9 )

= -12( a + 3 )( 2a - 3 )( 2a + 3 )

a. ( a² + b² - 5 )² - 2 ( ab + 2 )²

= ( a² + b² - 5 )² - [\(\sqrt{2}\)( ab + 2 ) ]²

= [ a² + b² - 5 -\(\sqrt{2}\)( ab + 2 ) ] [ a² + b² - 5 +\(\sqrt{2}\)( ab + 2 ) ]

= ( a² + b² - 5 -\(\sqrt{2}\)ab - 2\(\sqrt{2}\)) ( a² + b² - 5 +\(\sqrt{2}\)ab + 2\(\sqrt{2}\) )

b. ( 4a² - 3a - 18 )² - ( 4a² + 3a )²

= ( 4a² - 3a - 18 - 4a² - 3a ) ( 4a² - 3a - 18 + 4a² + 3a )

= ( - 6a - 18 ) ( 8a² - 18 )

= - 6 ( a + 3 ) . 2 [ ( 2a )² - 3² ]

= - 12 ( 2a - 3 ) ( 2a + 3 )

\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

\(a^3-b^3+3a^2+3ab+b^2\)

\(=\left(a-b\right)\left(a^2+ab+b^2\right)+3\left(a^2+ab+b^2\right)\)

\(=\left(a-b+3\right)\left(a^2+ab+b^2\right)\)