Quãng đường AB chia thành 2 đoạn AC và CB.Trên đoạn AC, xe chạy hết thời gian t1, trên đoạn CB xe chạy hết thời gian t2.Tính vận tốc trung bình trên từng đoạn AC,CB và trên quãng đường AB

Những câu hỏi liên quan
Một người đi từ A đến B gồm 2 đoạn Ab và CB hết thời gian là 4h30ph. Tính quãng đường AC, CB biết rằng vận tốc người đó đi trên qquangx đường AC là 30km/h, đi trên quãng đường CB là 20km/h và quãng đường Ac dài hơn CB là 10km
Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)
Đúng 3
Bình luận (0)
Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)
Đúng 2
Bình luận (0)
Một chiếc xe chuyển động trên đoạn đường AB trong thời gian t1 với tốc độ trung bình 30km/h. Sau đó xe tiếp tục chuyển động trên đoạn đường BC trong thời gian t2 với tốc độ trung bình 20km/h. Biết t1 t2. Tìm tốc độ trung bình của xe trên toàn bộ quãng đường AC ? Bài này hơi kkhoó vì ko có thời gian nên mong mb giúp mik
Đọc tiếp
Một chiếc xe chuyển động trên đoạn đường AB trong thời gian t1 với tốc độ trung bình 30km/h. Sau đó xe tiếp tục chuyển động trên đoạn đường BC trong thời gian t2 với tốc độ trung bình 20km/h. Biết t1 = t2. Tìm tốc độ trung bình của xe trên toàn bộ quãng đường AC ?
![]() Bài này hơi kkhoó vì ko có thời gian nên mong mb giúp mik
Bài này hơi kkhoó vì ko có thời gian nên mong mb giúp mik
\(S_1=v_1t_1=30.t_1\left(km\right)\)
\(S_2=v_2t_2=20t_2\left(km\right)\)
\(v_{tb}=\frac{\left(S_1+S_2\right)}{t_1+t_2}=\frac{\left(30t_1+20t_2\right)}{2t_2}=\frac{50t_2}{2t_2}=\frac{25km}{h}\)
Đúng 0
Bình luận (0)
ta có:
thời gian người đó đi trên 1/2 thời gian đầu là:
Đúng 0
Bình luận (0)
MỘt người đi quãng đường AB gồm 1 đoạn AC và CB.Lúc đi,vận tốc trên đoạn AC là 12km/giờ,vận tốc trên CB là 8km/giờ thời già đi từ A đến B hết 3 giờ 30 phút.Lúc về ,vận tốc trên BC là 30km/giờ,vận tốc trên CA là 20 km/giờ thời gian về từ B về A hết 1 giờ 36 phút.Tính quãng đường AB.
Một chiếc xe chuyển động trên quãng đường AB trong thời gian t1,với tốc độ trung bình v1=30km/h.Xe tiếp tục chuyển động trên quãng đường BC trong thời gian t2 với tốc độ trung bình là 20km/h.Biết t1=t2.Tìm tốc độ trung bình của xe trên cả quãng đường AC.
Một người đi xe máy từ A đến B gồm hai quãng đường AC và CB hết tổng thời gian là 4 giờ 20 phút. Biết quãng đường AC ngắn hơn quãng đường CB là 20km, vận tốc của người đi xe máy trên quãng đường AC là 30 km/giờ và đi trên quãng đường CB là 20km/giờ. Tìm độ dài quãng đường AB.
Ta có: 4 giờ 20 phút= 13/3 giờ
Gọi độ dài quãng đường AC là x(km)
Gọi độ dài quãng đường CB là y(km)
Điều kiện x > 0 và y > 20
Lúc đó thời gian người đi xe máy đi trên quãng đường AC là x/30 (giờ)
Thời gian người đi xe máy đi trên quãng đường CB là y/20 (giờ)
Theo đề bài, thời gian cả thảy đi từ A đến B là 4 giờ 20 phút nên ta có phương trình:
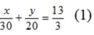
Vì quãng đường AB ngắn hơn quãng đường BC là 20 km nên ta có phương trình: y – x = 20 (2)
Từ (1) và (2) ta có hệ phương trình:


Vậy quãng đường AC dài 40km, quãng đường CB dài 60km.
Đúng 0
Bình luận (0)
1 người đi quãng đường AB gồm hai đoạn AC và CB .Lúc đi ,vận tốc trên đoạn AC là 12km/h, vận tốc trên đoạn CB là 8km/h ,hết 3h30p.Lúc về vận tốc trên đoạn BC là 30km/h ,vận tốc trên đoạn CA là 20km/h ,hết 1h36p.Tính quãng đường AB.
1 người đi quãng đường AB gồm hai đoạn AC và CB .Lúc đi ,vận tốc trên đoạn AC là 12km h, vận tốc trên đoạn CB là 8km h ,hết 3h30p.Lúc về vận tốc trên đoạn BC là 30km h ,vận tốc trên đoạn CA là 20km h ,hết 1h36p.Tính quãng đường AB.
Một người đi xe máy trên đoạn đường ABC. Biết đoạn đường AB trong thời gian t1 = 1 phút, người đó đi đoạn đường với vận tốc 16km/h, trên đoạn đường BC, người đó đi với vận tốc 24km/h, trong thời gian t2= 2 phút. Tính :
Vận tốc trung bình trên đoạn đường?
Đổi 1 phút = \(\dfrac{1}{60}\)h ; 2 phút = \(\dfrac{1}{30}\)h
Quãng đường AB dài :
\(\dfrac{1}{60}.16=\dfrac{4}{15}\left(km\right)\)
Quãng đường AB dài :
\(\dfrac{1}{30}.24=\dfrac{4}{5}\left(km\right)\)
Vận tốc TB trên cả đoạn đường là :
\(v_{tb}=\dfrac{s_1+s_2}{t_1+1_2}=\dfrac{\dfrac{4}{15}+\dfrac{4}{5}}{\dfrac{1}{60}+\dfrac{1}{30}}=\dfrac{64}{3}\approx21,3333\left(\dfrac{km}{h}\right)\)
Đúng 2
Bình luận (1)
Một người đi xe máy từ A đến B gồm 2 quãng đường AC và CB hết tổng thời gian là 4 giờ 30 phút. Biết vận tốc của người đó đi trên quãng đường lớn hơn vận tốc trên quãng đường CB là 20km/h và quãng đường AC dài hơn quãng đường CB là 10km
Lời giải:
Đổi 4h30 = $4,5$ h
Vận tốc trên quãng đường CB là $a$ km/h thì vận tốc trên $AC$ là $a+20$ (km/h)
Quãng đường $AC=BC+10$ (km)
Tổng thời gian đi quãng đường AB: $\frac{AC}{v_{AC}}+\frac{CB}{v_{CB}}=4,5$
$\Leftrightarrow \frac{BC+10}{a+20}+\frac{BC}{a}=4,5$
Khai thác được đến đây thì không biết bạn muốn tìm cái gì?
Đúng 0
Bình luận (0)


















