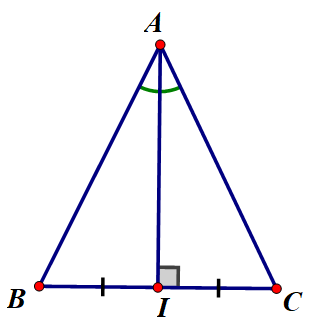
Chứng minh định lí:' Nếu tam giác có 1 đg trung tuyến đồng thời là đg trung trực ứng vs cùng 1 cạnh thì tam giác đó là tam giác cân '. Ai lm nhanh mk đúng thì mk tick cho ![]()
![]()

Những câu hỏi liên quan
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.
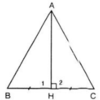
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
Đúng 0
Bình luận (0)
Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân
Hướng dẫn:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Đúng 0
Bình luận (1)
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:
HB = HC
= 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Đúng 0
Bình luận (0)
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:
HB = HC
\(\widehat{H_1}=\widehat{H_2}\) = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:
HB = HC
= 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Đúng 0
Bình luận (0)
chứng minh định lý nếu tam giác có một đg trung tuyến đồng thời là đg phân giác thì tam giác đó cân
giả sử đó là tam giác abc, am là trugn tuyến của tam giác abc =>mb=mc
vì am là đg phân giác => góc mab = góc mac
Xét tam giác amb và tam giác amc có:
góc mab = góc mac(cmt)
mb=mc (cmt)
am chung
=> tam giác amb= tam giác amc(c.g.c)
=> <mab=<mac( hia cạnh tg ứng)
xét tam giác abc có <b=<c (chứng minh trên)
= tam giác abc cân
Đúng 0
Bình luận (0)
Chứng minh định lý : Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
= 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Đúng 0
Bình luận (0)
xét tam giác AMB và tam giác AMC, có:
AB=AC
MB=MC(gt)
AM chung
=>tam giác AMB= tam giác AMC (c.c.c)
M1=M2 mà góc M1+góc M2=180 độ
=>góc M1= góc M2= góc MC=90 độ
=>AM vuông góc với BC
mà MA=MB
=>AM là đường trung trực của tam giác ABC
Yên tâm đi chắc chắn đúng
Đúng 0
Bình luận (0)
Nhận xét Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.Từ nhận xét trên hãy chứng minh: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
Đọc tiếp
Nhận xét
Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.
Từ nhận xét trên hãy chứng minh: "Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân "
ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
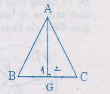
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
chứng minh rằng trong một tam giác có 1 đg trung tuyến đồng thời là đg phân giác thì tam giác đó cân
Chứng minh định lý : Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thig tam giác đó là một tam giác cân.
Thử coi, chả biết đúng không. Không đúng cho t xin lỗi nha
Giả dụ đề: Cho tam giác ABC có AM vừa là trung tuyến vừa là đường trung trực
Chứng minh: tam giác ABM = tam giác ACM
Xét tam giác ABM và tam giác ACM có:
\(\hept{\begin{cases}BM=CM\left(gt\right)\\AM:chung\\\widehat{AMB}=\widehat{AMC}=90^0\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
\(\Rightarrow AB=AC\)(hai cạnh tương ứng)
\(\Rightarrow\Delta ABC\)cân tại \(A\)
hay:
\(\Rightarrow\widehat{ABM}=\widehat{ACM}\)(hai góc tương ứng)
\(\Rightarrow\Delta ABC\)cân tại \(A\)
Đúng 0
Bình luận (0)
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH \(\perp\)BC và HB = HC
Xét 2 tam giác vuông HAB và HAC ta có
HB = HC
\(\widehat{H_1}\)= \(\widehat{H_2}\)= 900
AH : cạnh chung
Nên \(\Delta HAB\)=\(\Delta HAC\)=> AB = AC
Nên \(\Delta ABC\) cân tại A
1. Hãy chứng minh định lý: trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
2. Hãy chứng minh định lí: nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Giúp mình với!
Ai nhanh 3 tick
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)
Đúng 0
Bình luận (0)
Chứng minh định lí : Nếu tam giác có đường trung tuyến đồng thời là đường trung trực ứng với một cạnh thì tam giác đó là một tam giác cân.
Lâu lâu đăng một bài cho vui thôi, nhớ trả lời câu trả lời của mình nha ^^
Bạn ơi mik nên tahm khảo tại link này nhé :
https://h.vn/hoi-dap/tim-kiem?
Bạn đánh ra trên hoc.vn24 các bạn ý giải cho
ình quên các anh chị
~Hok tốt`
Đúng 0
Bình luận (0)
Bài toán:
Cho tam giác ABC có AH đồng thời là đường trung tuyến,đồng thời là đuờng trung trực.Chứng minh rằng tam giác ABC cân.

Xét \(\Delta AHB\) và \(\Delta AHC\) ta có:
\(AH\) chung.
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(HB=HC\)
\(\Rightarrow\Delta AHB=\Delta AHC\left(g.c.g\right)\Rightarrow\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta ABC\) cân.
Đúng 0
Bình luận (0)
Cm: C1: Xét t/giác ABH và t/giác ACH
có AH : chung
\(\widehat{H_1}=\widehat{H_2}=90^0\) (gt)
BH = CH (gt)
=> t/giác ABH = t/giác ACH (c.g.c)
=> AB = AC (2 cạnh t/ứng)
=> t/giác ABC cân tại A
=> Đpcm
C2. Ta có: AH là đường trung trực của BC
=> AH \(\perp\)BC , mà BH = HC (gt)
=> AB = AC (quan hệ giữa đường xiên và hình chiếu)
=> t/giác ABC cân tại A
=> Đpcm .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời