Tính tổng A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64

Những câu hỏi liên quan
A=1/2+1/4+1/8+1/16/1/32+1/64
tính tổng
nhân A lên 2A sau đó lấy 2A-A là đc :
2A =1+1/2+.....+1/32
2A-A=(1+1/2+.....+1/32)-(1/2+1/4+.....+1/32+1/64)
A=1-1/64
A=63/64
Đúng 0
Bình luận (0)
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(2A=\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\times2\)
\(2A=\frac{1}{2}\times2+\frac{1}{4}\times2+\frac{1}{8}\times2+\frac{1}{16}\times2+\frac{1}{32}\times2+\frac{1}{64}\times2\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(2A-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\)
\(A=1-\frac{1}{64}\)
\(A=\frac{63}{64}\)
Đúng 0
Bình luận (0)
5 tính tổng sau bằng cách hợp lý.b,A= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
Lời giải:
$A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$
$2\times A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}$
$2\times A-A=(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32})-(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64})$
$A=1-\frac{1}{64}=\frac{63}{64}$
Đúng 2
Bình luận (0)
A=1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
2A = 2.(1/2+1/4+1/8+1/16+1/32+1/64)
= 1 + 1/2+1/4+1/8+1/16+1/32
=> 2A - A = (1+1/2+1/4+1/8+1/16+1/32) - (1/2+1/4+1/8+1/16+1/32+1/64)
=> A = 1 - 1/64
= 63/64
Đúng 2
Bình luận (0)
Tính tổng: S= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
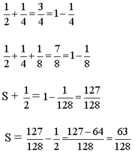
Đúng 0
Bình luận (0)
tính tổng
1=1/2+1/4+1/8+1/16+1/32+1/64
Ta có : A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
=> 2A = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32
=> 2A - A = 1 - 1/64
=> A = 1 - 1/64
=> A = 63/64
Đúng 0
Bình luận (0)
Tính tổng:
1/2+1/4+1/8+1/16+1/32+1/64+1/128
Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(\Rightarrow2A-A=1-\frac{1}{128}=\frac{127}{128}\)
Đúng 0
Bình luận (0)
Tính nhanh tổng sau:
B= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
B= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
B=1/2+1/2^2+1/2^3+1/2^4+1/2^5+1/2^6
=>2B=1+1/2+1/2^2+...1/3^5
=>2B-B=1-1/2^6
=>B=1-1/64
=>B=63/64
tính tổng dãy phân số sau
1/2+1/4+1/8+1/16+1/32+1/64
- Tính A x 2
A x 2 = 1 + 1/2 +1/4 +1/8 +1/16+ 1/32
- Tính A bằng cách A = A x 2 – A
Vậy A = 1 + 1/2 +1/4 +1/8 +1/16+ 1/32 - 1/2 - 1/4 - 1/8 -1/16 - 1/32 - 1/64
A = 1 - 1/64
A = 63/64
Đúng 0
Bình luận (0)
Đặt A=1/2+1/8+1/16+1/32+1/64.Ta có:
A x 2=(1/2+1/8+1/16+1/32+1/64) x 2
A x 2=1+1/2+1/4+1/8+1/16+1/32
A x 2-A=(1+1/2+1/4+1/8+1/16+1/32)-(1/2+1/4+1/8+1/16+1/32+1/64)
A=1-1/64=63/64
Ai đi qua cho mình xin cái k mình k lại cho
Đúng 0
Bình luận (0)
- Tính A x 2
A x 2 = 1 + 1/2 +1/4 +1/8 +1/16+ 1/32
- Tính A bằng cách A = A x 2 – A
Vậy A = 1 + 1/2 +1/4 +1/8 +1/16+ 1/32 - 1/2 - 1/4 - 1/8 -1/16 - 1/32 - 1/64
A = 1 - 1/64
A = 63/64
Đúng 0
Bình luận (0)
tính tổng :
S = 1/2 + 1/4 +1/8 + 1/16 +1/32 +1/64 . ( bài tính nhanh đấy , giúp mình nhé )
S=1/2+1/4+1/8+1/16+1/32+1/64
S=1-1/2+1/2-1/4+1/4-1/8+1/8-1/16+1/16-1/32+1/32-1/64
S=1-1/64
S=63/64
Đúng 0
Bình luận (0)
S = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
2S = 1/2 x 2 +1/4 x 2 + 1/8 x 2 + 1/16 x 2 + 1/32 x 2 + 1/64 x 2
2S =1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32
2S - S = ( 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 ) - ( 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 )
S = 1 - 1/64
S = 63/64
Đúng 0
Bình luận (0)
Tính: A = 1/2+1/4+1/8 + 1/16 + 1/32 + 1/64.
Xem chi tiết
Tính không quy đồng mẫu:
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+...+\frac{1}{32}-\frac{1}{64}\)
\(A=1-\frac{1}{64}=\frac{63}{64}\)
Đúng 1
Bình luận (0)
A = 32 + 16 + 8 + 4 + 2 + 1/64 = 63/64
Đúng 3
Bình luận (0)
P/s nhỏ
Bạn vào câu hỏi tương tự nhé
Có nhiều câu giồng bạn lắm
Học tốt nhé!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời




























