CM ''bất đẳng thức tam giác mở rộng '':Với 3 điểm A,B,C bất kì ,ta có :AB+AC lớn hơn hoặc bằng BC

Những câu hỏi liên quan
Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
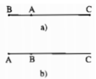
- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.
Trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
• Nếu A nằm giữa B và C thì AB + AC = BC.
• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.
Suy ra: AC + AB > BC
• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.
Suy ra: AB + AC > BC.
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC
Đúng 0
Bình luận (0)
Chứng minh "bất đẳng thức tam giác mở rộng" : Với ba điểm A, B, C bất kì ta có :
\(AB+AC\ge BC\)
Xét 2 trường hợp:
+ A, B, C thẳng hàng và A nằm giữa B và C:
Khi đó AB + AC = BC
+ A, B, C không thẳng hàng hay A, B, C thẳng hàng nhưng A không nằm giữa B và C:
Khi đó AB + AC > BC
Vậy \(AB+AC\ge BC\)
Đúng 0
Bình luận (0)
1/ Hãy tìm cạnh của t/g cân, nếu 2 cạnh của nó bằng :a ) 7cm và 3cmb) 8cm và 2cmc) 10cm và 5 cm2/ Chứng minh trong 1 đường tròn, đường kính là dây lớn nhất :3/ Chứng minh bất đẳng thức tam giác mở rộng Với 3 điểm A, B, C bất kì ta có :AB + AC hoặc BC4/ Cho đường thẳng d và điểm A, B nằm cùng phía của d va AB // d. Một điểm M di động trên d. Tìm vị trí của M sao cho |MA - MB|là lớn nhất ( Các bạn giải đc 2 câu là mình sẽ tick nhanh nhất có thể nhé, Thanks )
Đọc tiếp
1/ Hãy tìm cạnh của t/g cân, nếu 2 cạnh của nó bằng :
a ) 7cm và 3cm
b) 8cm và 2cm
c) 10cm và 5 cm
2/ Chứng minh trong 1 đường tròn, đường kính là dây lớn nhất :
3/ Chứng minh "bất đẳng thức tam giác mở rộng" Với 3 điểm A, B, C bất kì ta có :
AB + AC > hoặc = BC
4/ Cho đường thẳng d và điểm A, B nằm cùng phía của d va AB // d. Một điểm M di động trên d. Tìm vị trí của M sao cho |MA - MB|
là lớn nhất
( Các bạn giải đc 2 câu là mình sẽ tick nhanh nhất có thể nhé, Thanks )
Cho tam giác ABC,ta có các bất đẳng thức
AB+BC lớn hơn AC
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.Mình giải cách sau có đúng ko?--Ta có: MB+MAAB (Bất đẳng thức tam giác) MC+MBBC (Bất đẳng thức tam giác) MA+MCAC (Bất đẳng thức tam giác) MB+MA+MC+MB+MA+MCAB+BC+AC 2MA+2MB+2MC 2P MA+MB+MC P (được phần CM)--Ta có: MA+ABMB (Bất đẳng thức tam giác) MB+BCMC (Bất đẳng thức tam giác) MC+ACMA (Bất đẳng...
Đọc tiếp
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
Cho tam giác đều ABC có cạnh bằng a, gọi M là điểm bất kì trên cạnh BC (M khác B,C). Vẽ góc xMy bằng 60 độ sao cho hai cạnh Mx, My luôn cắt cạnh AB,AC lần lượt tại D và E. Chứng minh bất đẳng thức: BD.CE<=a^2/4
Xem chi tiết
Cho tam giác đều ABC, cạnh bằng 3. M là điểm bất kì trong tam giác. Qua M kẻ các đường thẳng song song với AB,BC,AC, chúng cắt BC,CA,AB theo thứ tự ở A',B',C'. Ta có MA'+MB'+MC'=
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.Mình giải cách sau có đúng ko?--Ta có: MB+MAAB (Bất đẳng thức tam giác) MC+MBBC (Bất đẳng thức tam giác) MA+MCAC (Bất đẳng thức tam giác) MB+MA+MC+MB+MA+MCAB+BC+AC 2MA+2MB+2MC 2P MA+MB+MC P (được phần CM)--Ta có: MA+ABMB (Bất đẳng thức tam giác) MB+BCMC (Bất đẳng thức tam giác) MC+ACMA (Bất đẳng...
Đọc tiếp
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
Cho tam giác đều ABC, cạnh bằng 3 cm. M là điểm bất kì nằm trong tam giác. Qua M kẻ các đường thẳng song song với AB, BC, CA, chúng cắt BC, CA, AB theo thứ tự ở A', B', C'. Ta có MA' + MB' + MC' =













