
Mình đag cần rất rất gấp chi tiết 2 phần. mọi ng giúp mình vớiiiiiiiiiiiiiiii ak. mình cảm ơn trc

Tính GTNN
Mình đag cần rất rất gấp chi tiết 2 phần này. mọi ng giúp mình vớiiiiiiiiiii ak. mình cảm ơn trc ak
A=/x-1/+/x-3/+/x-5/+/x-7/=/x-1/+/3-x/+/x-5/+/7-x/>=/x-1+3-x/+/x-5+7-x/=4
dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-1>=0,3-x>=0\\x-5>=0,7-x>=0\end{cases}\Rightarrow\hept{\begin{cases}x>=1,3>=x\\x>=5,7>=x\end{cases}\Rightarrow}\hept{\begin{cases}1< =x< =3\\5< =x< =7\end{cases}}}\)
vậy 1<=x<=3 và 5<=x<=7
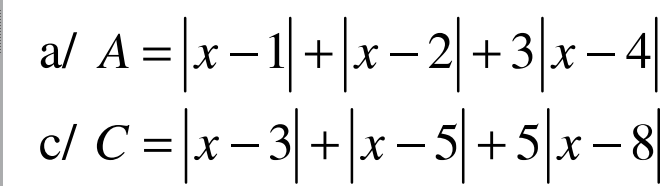
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
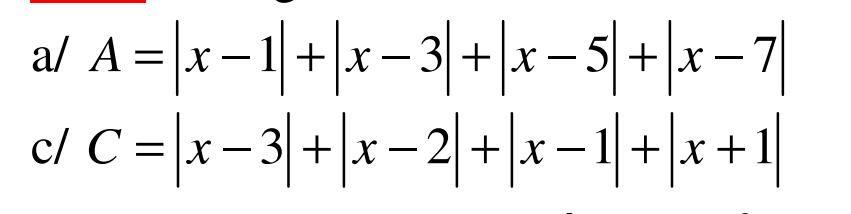
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
https://hoc24.vn/cau-hoi/minh-can-rat-rat-gap-loi-giai-chi-tiet-2-phan-nay-de-bai-la-tinh-gtnn-moi-ng-giup-minh-voiiiiiiiiiiiiiiiiiiiii-ak-minh-cam-on.1527826665808
Mình làm ở đây rồi bạn nhé. Bạn vào link này tham khảo.
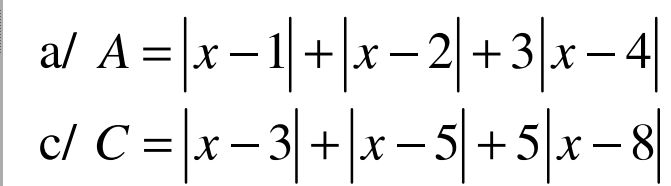
Tìm GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
a. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-4|=|x-1|+|4-x|\geq |x-1+4-x|=3$
$|x-2|+|x-4|=|x-2|+|4-x|\geq |x-2+4-x|=2$
$|x-4|\geq 0$
Cộng theo vế:
$A\geq 5$
Vậy $A_{\min}=5$. Giá trị này đạt tại \(\left\{\begin{matrix} (x-1)(4-x)\geq 0\\ (x-2)(4-x)\geq 0\\ x-4=0\end{matrix}\right.\Leftrightarrow x=4\)
c. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ thì:
$|x-3|+|x-8|=|x-3|+|8-x|\geq |x-3+8-x|=5$
$|x-5|+|x-8|=|x-5|+|8-x|\geq |x-5+8-x|=3$
$3|x-8|\geq 0$
Cộng theo vế:
$C\geq 8$. Vậy $C_{\min}=8$. Giá trị này đạt tại $x=8$
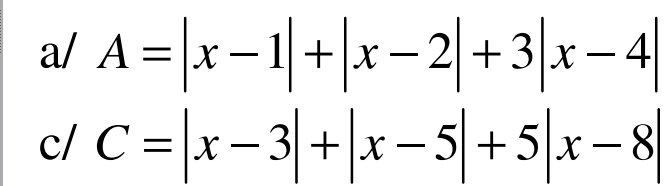
Tính GTNN
Mình cần rất rất gấp lời giải chi tiết 2 phần này. . Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
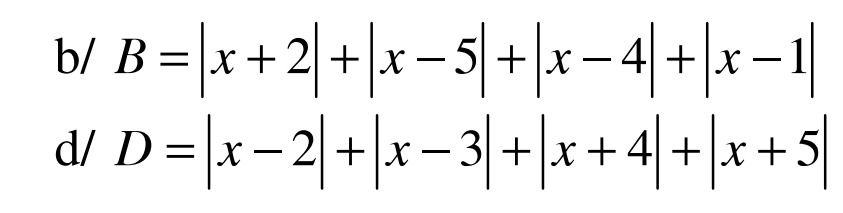
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn
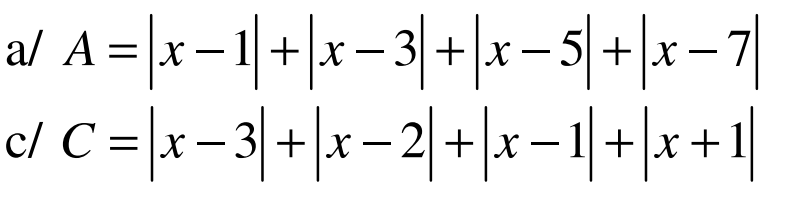
Mình cần rất rất gấp lời giải chi tiết 2 phần này. đề bài là tính GTNN. Mọi ng giúp mình vớiiiiiiiiiiiiiiiiiiiii ak. mình cảm ơn

Mình đag cần rất rất gấp. và mình cần chi tiết 2 phần. mọi ng giúp mình vớiiiiiiiiiiiiiii
Tính GTNN mn nha

Mình đag cần rât rất gấp. mọi ng giúp mình vớiii. mình cần lời giải chi tiết. giúpmình vớiiiiiii. mình cảm ơn
\(B=\left|x+1\right|+\left|x-4\right|+\left|2x-5\right|\ge\left|2x-3\right|+\left|2x-5\right|=\left|2x-3\right|+\left|5-2x\right|\)
\(\ge\left|2x-3+5-2x\right|=\left|2\right|=2\)
Dấu ''='' xảy ra khi \(\left(x+1\right)\left(4-x\right)\ge0;\left(2x-3\right)\left(5-2x\right)\ge0\)
\(-1\le x\le4;\frac{3}{2}\le x\le\frac{5}{2}\Rightarrow-1\le x\le4\)
Vậy GTNN của B bằng 2 tại -1 =< x =< 4