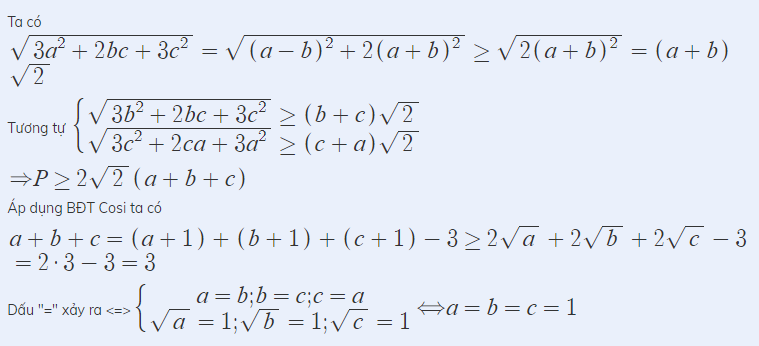tính a^2+b^2+c^2+2ab+2bc-2ac+a+b-c biết 2a+3b=7 và a+b+3c=12

Những câu hỏi liên quan
Tìm GTLN của B= \(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ac+3a^2}\)
Biết a,b,c >=0 và \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)3
xin lỗi nha MÌNH sai đề ở chổ \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
Đúng 0
Bình luận (0)
Cho \(a,b,c\ge0\) và \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
Tìm GTNN của \(A=\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ac+3a^2}\)
\(3x^2+2xy+3y^2=\left(x+y\right)^2+2\left(x^2+y^2\right)\ge\left(x+y\right)^2+\left(x+y\right)^2=2\left(x+y\right)^2\)
\(\Rightarrow A\ge\sqrt{2}\left(a+b\right)+\sqrt{2}\left(b+c\right)+\sqrt{2}\left(c+a\right)\)
\(A\ge2\sqrt{2}\left(a+b+c\right)\ge\frac{2\sqrt{2}}{3}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=6\sqrt{2}\)
\(A_{min}=6\sqrt{2}\) khi \(a=b=c=1\)
Đúng 0
Bình luận (0)
Ch ba số a,b,c khác 0 và ab+bc+ac=0
Tính giá trị của biểu thức A= ((a^2 / (a^2 + 2bc) + b^2 / (b^2 + 2ac) + c^2 / (c^2 + 2ba)) / (bc/(a^2 + 2bc) + ac/(b^2 + 2ac) + ab/(c^2+2ab))
chứng minh rằng 2 đa thức : 2bc(b+2c+2ac(c-2a)-2ab(a+2b-7a)=(b+2c)(c-2a)a+2b
Bạn có thể viết lại đề được không?Mình vẫn chưa rõ lắm.^^
Đúng 0
Bình luận (0)
Với mọi a,b,c, chứng minh:
a,\(a^4+b^4+c^4\ge a^2bc+b^2ac+c^2ab\)
b,\(a^4+b^4+c^4\ge a^3b+b^3c+c^3a\)
Cho các số thực a, b, c không âm thỏa \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\). Tìm GTNN của \(P=\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+3c^2}+\sqrt{3c^2+2ca+3a^2}\)
???????????????loằng ngoằng quá. Tui không hỉu cái GTNN
Đúng 0
Bình luận (0)
GTNN là tắt của giá trị nhỏ nhất,
Trong bài này bạn biến đổi sao cho biểu thức \(P\ge a\) (số a là số biết trước)
VD: Bạn đưa về dạng nào đó của biểu thức mà nó luôn lớn hơn hoặc bằng \(\dfrac{1}{3}\) Bạn có thể viết \(P\ge\dfrac{1}{3}\) thì GTNN của \(P=\dfrac{1}{3}\) hay \(minP=\dfrac{1}{3}\)
Tìm được GTNN rồi thì bạn tìm ẩn để dấu "=" xảy ra, nghĩa là để BĐT xảy ra dấu =, lúc đó biểu thức P đạt giá trị nhỏ nhất,
VD như: \(minP=\dfrac{1}{3}\) <=> Dấu = xảy ra
<=> x = b (x là ẩn và b là biết trước)
Ở một số bài có thể cho điều kiện của ẩn.
Đúng 0
Bình luận (0)
Cho a khác b, b khác c, c khác a và 1/a+1/b+1/c=0 Tính A= (bc/a^2+2bc) + (ca/b^2+2ac) + (ab/c^2 +2ab)
B = (a^2/ a^2 + 2bc) + (b^2/B^2+2ac) + (c^2/c^2+2ab)
Xem chi tiết
Phân tích đa thức thành nhân tử:
a) \(2bc\left(b+2c\right)+2ac\left(c-2a\right)-2ab\left(a+2b\right)-7abc\)
b) \(3bc\left(3b-c\right)-3ac\left(3c-a\right)-3ab\left(3a+b\right)+28abc\)
c) \(a\left(b^2+c^2\right)+b\left(a^2+c^2\right)+c\left(a^2+b^2\right)+2abc\)
Cô quản lí làm nhanh giúp e với ạ!!! BẠn e nhờ e gửi cho cô!!!
với a,b,c≥0 thỏa mãn \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\).Tìm GTNN của
Q=\(\sqrt{3a^2+2ab+3b^2}+\sqrt{3b^2+2bc+c^2}+\sqrt{3c^2+2ca+3a^2}\)