Cho hai điểm M,N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh tam giác AMN = tam giác BMN
Những câu hỏi liên quan
Cho 2 điểm M,N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh tam giác AMN= tam giác BMN
xét tam giác AMN và tam giác BMN có:
MA = MB ( M thuộc đường trung trực d)
NA = NB ( N thuộc đường trung trực d)
MN là cạnh chung
vậy tam giác AMN = tam giác BMN (c.c.c)
1 đúng nhé
Đúng 0
Bình luận (0)
Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Đúng 0
Bình luận (0)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB.
Chứng minh tam giác AMN = tam giác BMN
Do M,N nằm trên đường trung trực của đoạn AB
=>MA=MB(Tính chất đường trung trực)
NA=NB(Tính chất đường trung trực)
Xét tam giác AMN và tam giác BMN có:
MA=MB
NA=NB
MN chung
=>\(\Delta AMN=\Delta BMN\left(c.c.c\right)\left(đpcm\right)\)
Đúng 0
Bình luận (1)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Hướng dẫn:
Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Đúng 0
Bình luận (0)
47. Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh
∆AMN = ∆BMN.
Hướng dẫn:
Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Đúng 0
Bình luận (0)
Vì M nằm trên đường trung trực của AB nên MA = MB (Định lý 1)
Vì N nằm trên đường trung trực của AB nên NA = NB (Định lý 1)
Xét \(\Delta AMN\)và \(\Delta BMN\)có:
MA = MB (cmt)
NA = NB (cmt)
MN chung
\(\Rightarrow\Delta AMN=\Delta BMN\) (c.c.c)
Đúng 0
Bình luận (0)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Đúng 0
Bình luận (0)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Đúng 0
Bình luận (0)
Vì M, N thuộc đường trung trực của AB nên MA = MB; NA = NB
Xét tam giác AMN và tam giác BMN có:
MA = MB
NA = NB
MN chung
=> Tam giác AMN = Tam giác BMN (c.c.c)
Đúng 0
Bình luận (0)
vì M và N nằm trên đường trung trực của AB nên M và N cách đều 2 điểm A và B, hay AN=NB; AM=MB.
xát tam giác ANM và tam giác BNM có:
AN=NB (cmt)
AM=MB(cmt)
MN: chung
do đó tam giác ANM= tam giác BNM (c-c-c)
Đúng 0
Bình luận (0)
cho đường thẳng d là đường trung trực AB . M;N thuộc d . chứng minh tam giác AMN = tam giác BMN bằng 3 cách (g.c.g ; c.c.c; c.g.c)
Giúp mk với
Gọi O là giao điểm của AB và d
Vì d là đường trung trực (đtt ) của AB => Tam giác AOM = tam giác BOM ( c.g.c )
=> Tam giác AON = tam giác BOM ( c.g.c )
=> AM = BM và AN = BN, g AMN = g BMN, g ANO = g BNO hay g ANM = g BNM
Từ những điều kiện trên ta suy ra:
=> tam giác AMN = tam giác BMN ( c.c.c )
=> tam giác AMN = tam giác BMN ( c.g.c )
=> tam giác AMN = tam giác BMN ( g.c.g )
( Đây là lời giải tóm tắt của mik, bạn nhớ giải đầy đủ ra nhé )
Đúng 0
Bình luận (0)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
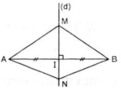
Vì M thuộc đường trung trực của AB
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)
Đúng 0
Bình luận (0)
Tam giác AMB cân tại M có góc M là 100 độ. Trên đường trung trực của đoạn thẳng AB lấy điểm N sao cho điểm M nằm trong tam giác ABN.
Tính góc AMN
Bài 1 : Cho tam giác cân ABC (AB = AC). Trên AB lấy D và trên AC lấy E sao cho AD = AE .
Bài 2 : Cho đoạn thẳng AB. Vẽ hai đường tròn có bán kính bằng nhau tâm tại A và B sao cho chúng cắt nhau tại M và N.
a) Chứng minh rằng AMN = BMN.
b) Chứng minh rằng MN là đường trung trực của đoạn AB