Cho AB và CD là hai đoạn thẳng song song và bằng nhau, A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. Chứng minh rằng A'B' = C'D'
GIÚP MK VS NHA. CẢM ƠN MỌI NGƯỜI NHIỀU Ạ
@soyeon_Tiểubàng giải
Cho AB và CD là hai đoạn thẳng song song và bằng nhau , A'B' và C'D' là hình chiếu của chúng trên cùng 1 đường thẳng . CM A'B'=C'D'
Cho AB và CD là hai đoạn thẳng song song và bằng nhau, A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. Chứng minh rằng A'B' = C'D'
GIÚP MK VS NHA. CẢM ƠN MỌI NGƯỜI NHIỀU Ạ
@soyeon_Tiểubàng giải
1 câu trả lời
Toán lớp 7 Ôn tập toán 7

Từ A hạ đường vuông góc với BB' tại H
Từ C hạ đường vuông góc với DD' tại K
Gọi I là giao điểm của CD và BB'
Dễ thấy BB' // DD' do cùng _|_ A'D'
=> BID = IDK (so le trong)
Lại có: ABI = BID (so le trong)
=> IDK = ABI
Xét t/g ABH vuông tại H và t/g CDK vuông tại K có:
AB = CD (gt)
ABH = CDK (cmt)
Do đó, t/g ABH = t/g CDK ( cạnh huyền - góc nhọn)
=> AH = CK (2 cạnh tương ứng) (1)
Có: AH // A'B' ( cùng _|_ BB')
AA' // B'H ( cùng _|_ A'D')
=> AH = A'B' ( tính chất đoạn chắn) (2)
Tương tự ta cũng có: CK = C'D' (3)
Từ (1); (2) và (3) => A'B' = C'D' (đpcm)
Bài này có trong câu hỏi tương tự bạn nên tìm nhé :)))
Mình dán lên đây cho bạn xem cho tiện
Cho AB // CD và AB = CD ,. A'B' và C'D' là các hình chiếu của chúng trên cùng một đường thẳng. CMR A'B'=C'D'
Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN= PQ.
Hai đoạn thẳng AB = 35cm, CD = 105cm tỉ lệ với hai đoạn thẳng A'B' = 75cm và C'D'
Đoạn thẳng C'D' có độ dài (theo đơn vị cm) là :
A. 25
B. 49
C. 225
D. 315
Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng A'B' và C'D' ?
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:
\(\dfrac{AB}{CD}=\dfrac{A'B'}{C'D'}hay\dfrac{AB}{A'B}=\dfrac{CD}{C'D'}\)
Phát biểu và viết tỉ lệ thức biểu thị hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thằng A'B' và C'D'.
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:

Cho AB và CD là 2 đoạn thẳng song song và bằng nhau,A`B`và C`D`là các hình chiếu của chúng trên cùng 1 dường thẳng.Chứng minh A`B`=C`D`
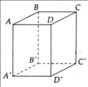
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ trên.
a) Nêu vị trí tương đối của các cặp đường thẳng AB' và C'D; B'D' và AD; AC và A'C.
b) BC’ song song với (ADD'A') không? Vì sao? Chứng minh (BCC'B') song song với (ADD'A').
c) AC' và CA'có cắt nhau không? Vì sao?
d) Hai mặt phẳng (ACC'A') và (BDD'B') có cắt nhau không? Nếu cắt thì cắt theo đường thẳng chung nào?
Tương tự 1A
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
Bài 19: Cho tam giác ABC có AC > AB. M là một điểm bất kỳ trên cạnh BC. Tìm vị trí
điểm M sao cho AM có độ dài nhỏ nhất.
Bài 20: Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN PQ.
Bài 21: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC ( H BC). Chứng minh:
AH + BC > AB + AC.