Cho tam giác ABC gọi M và N lần lượt là trung điểm của AB và AC
CM : MN//BC và MN = 1/2 BC
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
=
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu củ
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQMa A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc A
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
QM
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
tóm lị là ABGHMN là sai
Giải giúp mik vs ạ
Thank you ♥️
Cho tam giác ABC có AB = 12cm, AC = 16 cm, BC = 20 cm. 1. Tam giác ABC là tam giác gì? 2. Lấy M, N lần lượt trên AB, AC sao cho AM = 3cm, AN = 4cm. CMR: MN // BC 3. Gọi I là trung điểm BC. G là giao điểm của AI và MN. CMR: G là trung điểm MN
Cho tam giác ABC có BC = 16 cm. Gọi D và E lần lượt là trung điểm của AB và AC. Gọi M và N lần lượt là trung điểm của BD và EC. Tính MN?
A. 9cm
B. 8cm
C. 10cm
D. 12cm
* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
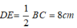
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D
1 ) cho tam giác ABC có AB=AC . trên các cạnh AB,AC lần lượt lấy các điểm E và F sao cho AE = AF
cm : AF // BC
2) cho tam giác ABC có M và N lần lượt là trung điểm của AB , AC
cm : MN // BC và MN = 1 phần 3 BC
cho tam giác ABC là tam giác nhọn ( AB< AC). Gọi M và N lần lượt là trung điểm của AB và AC.
a) Chứng minh MN // BC
b) Biết BC = 12 cm. Tính MN
c) Chứng minh tứ giác BMNC là hình thang
a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC
b, Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC=6\left(cm\right)\)
c, Vì MN//BC nên BMNC là hình thang
Cho tam giác ABC, gọi M và N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MN lấy điểm E sao cho MN = NE
a. CM MB= CE và MB // CE
b. CM tam giác MCB= tam giac CME
c. CM MN=1/2 BC,MN//BC
cho tam giác ABC gọi MN lần lượt là trung điểm AB của BA và BC CMR MN//AC và MN=1/2 BC
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
nhé !
Bài 1:
Cho tam giác ABC;M là trung điểm BC.Kẻ MN//AB;N thuộc AC
Cm: a) N là trung điểm AC
b) MN=1/2AB
Bài 2:
Cho tam giác ABC gọi G là trọng tâm của tam giác ABC,M là trung điểm BC.Kẻ đường thẳng qua G//BC cắt AB,AC lần lượt tại D và E
a) cm: G là trung điểm DE
b) Tính tỉ số DE/BC=?
vẽ giúp mình hình luônn nhess
Cho 2 cái hình vì con chưa hc lp 8.
Bài 1
Bài 2 :
Bài 1:
Mượn hình bạn kia luôn nhé!
a) Vì M là trung điểm BC và MN//AB
=> N là trung điểm của AC (tính chất của đường trung bình)
b) Vì M là trung điểm của BC, N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> \(MN=\frac{1}{2}AB\)
Cho tam giác ABC ( AB < AC ). Gọi MN lần lượt là trung điểm của AB, AC
a) Cm: MN // BC và tính BC biết MN = 4cm
b) Gọi I là điểm đối xứng N qua M. Chứng minh tứ giác AIBN là hình bình hành
c) Gọi E là trung điểm của BN. Tia ME cắt BC tại K, Chứng minh E là trung điểm MK
d) Gọi D là giao điểm của AE và BC. Chứng mình BD=1/3 BC