tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu
Những câu hỏi liên quan
24 tháng 12 2016 lúc 11:21
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
24 tháng 12 2016 lúc 22:01
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
áp dụng công thức \(C^k_n=\frac{n!}{k!.\left(n-k\right)!}\)
rồi giải pt là ra
nhưng pt này vô nghiệm
Đúng 0
Bình luận (0)
23 tháng 12 2016 lúc 23:32
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
25 tháng 12 2016 lúc 19:09
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
25 tháng 12 2016 lúc 14:52
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
25 tháng 12 2016 lúc 10:34
tổng các nghiệm của phương trình \(C^4_n+C^5_n=C^6_n\) ( n thuộc N*) là bao nhiêu ?
a. CMR: A = căn 2 + căn 3 là số vô tỉ
b. Cho căn n là nghiệm của phương trình: x3+ax2+bx+c = 0 ( a, b, c thuộc Q ), n là số tự nhiên không chính phương. Tìm các nghiệm còn lại.
a. CMR: A = căn 2 + căn 3 là số vô tỉ
b. Cho căn n là nghiệm của phương trình: x3+ax2+bx+c = 0 ( a, b, c thuộc Q ), n là số tự nhiên không chính phương. Tìm các nghiệm còn lại
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
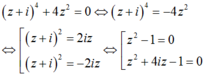
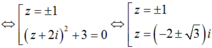
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đúng 0
Bình luận (0)