tìm trên mặt phẳng tọa độ các điểm: a, có tung độ bằng -1 b,có hoành độ bằng 2

Những câu hỏi liên quan
trên mặt phẳng tọa độ Oxy vẽ điểm A có tọa độ (1;1) đường tròn tâm A với bán kín Oa cắt các tia õ,oy theo thứ tự B và C tìm tọa độ của các điểm B và C
Trên mặt phẳng tọa độ Oxy, vẽ điểm A có tọa độ (1;1). Đường tròn tâm O với bán kinh Oa cắt các tia Ox, Oy theo thứ tự B và C. Tìm tọa độ của các điểm B, C.
Lời giải:
Áp dụng định lý Pitago: $OA=\sqrt{1^2+1^2}=\sqrt{2}$
Vì $B\in Ox$ nên tọa độ của $B$ có dạng $(b,0)$
Vì $B$ thuộc đường tròn tâm $O$ bán kính $OA=\sqrt{2}$ nên $|x_B|=OB=OA=\sqrt{2}$. Vậy $B(\pm \sqrt{2},0)$
$C\in Oy$ nên $C$ có tọa độ $(0,c)$
$C$ thuộc đường tròn đường kính $OA$ nên:
$|y_C|=OC=OA=\sqrt{2}$. Vậy $C(0, \pm \sqrt{2})$
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có hoành độ bằng 0
Các điểm có hoành độ bằng 0 là những điểm nằm trên trục tung.
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có hoành độ bằng 2
Các điểm có hoành độ bằng 2 là những điểm nằm trên đường thẳng song song với trục Oy, cắt trục hoành là điểm có hoành độ bằng 2 (đường thẳng x =2)
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có tung độ bằng 0
Các điểm có tung độ bằng 0 là những điểm nằm trên trục hoành.
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có tung độ bằng 5
Các điểm có tung độ bằng 5 là những điểm nằm trên đường thẳng song song với trục Ox, cắt trục tung là điểm có tung độ bằng 5 (đường thẳng y = 5)
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có tung độ và hoành độ đối nhau
Các điểm có tung độ và hoành độ đối nhau là những điểm nằm trên đường thẳng chứa tia phân giác của góc x’Oy hay phân giác góc vuông số II và góc vuông số IV (đường thẳng y = -x)
Đúng 0
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm: Có tung độ và hoành độ bằng nhau
Các điểm có tung độ và hoành độ bằng nhau là những điểm nằm trên đường thẳng chứa tia phân giác của góc xOy hay phân giác góc vuông số I và góc vuông số III (đường thẳng y = x)
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho điểm M có tọa độ ( x 0 ; y 0 ; z 0 ). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).
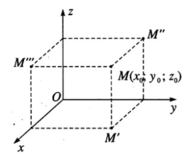
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )
Đúng 0
Bình luận (0)






