Chứng minh rằng : 9797 - 7979 là số chẵn?
chứng minh rằng tích của hai hay nhiều số chẵn là 1 số chẵn
a) Chứng minh rằng: Tích của hai số chẵn liên tiếp thì chia hết cho 8
b) Chứng minh rằng: Tích của ba số chẵn liên tiếp thì chia hết cho 48
c) Chứng minh rằng: Tích của bốn số chẵn liên tiếp thì chia hết cho 384
bạn hãy áp dụng công thức này mà làm: k.(k+1)....(k+n) luôn chia hết cho 1,2,...,n+1 biết k và n là số nguyên
gọi 2 số chẵn liên tiếp đó là: 2k,2k+2
2k.(2k+2)=4k(k+1) mà k(k+1) chia hết cho 2 suy ra 2k.(2k+2) chia hết cho 8
gọi 3 số chẵn liên tiếp đó là: 2k,2k+2,2k+4
2k.(2k+2)(2k+4)=8k(k+1)(k+2) mà k(k+1) chia hết cho 2 suy ra 2k.(2k+2)(2k+4) chia hết cho 16 (1)
k(k+1)(k+2) chia hết cho 3 suy ra 8k(k+1)(k+2) chia hết cho 3 suy ra 2k.(2k+2)(2k+4) chia hết cho 3 (2)
từ (1),(2) suy ra 2k.(2k+2)(2k+4) chia hết cho 48 do (16,3)=1
câu c, tương tự vậy
ASDWE RHTYJNHWSAVFGB
a)Chứng minh rằng tích số lẻ là 1 số lẻ
b) Chứng minh rằng tổng 2 số lẻ là 1 số chẵn
giúp mình với!
Gọi 2 số lẻ là 2k+1 và 2h+1
Tích chúng là:
\(\left(2k+1\right)\left(2h+1\right)=4kh+2k+2h+1=2.\left(2kh+k+h\right)+1\) là 1 số lẻ => đpcm
Chứng minh rằng tổng của hai hàm số chẵn là một Hàm số chẵn, tổng hai hàm số lẻ là một Hàm số lẻ
Chứng minh rằng hàm số f(x) cho bởi
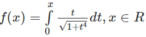
là hàm số chẵn.
Cho số tự nhiên n. Chứng minh rằng: nếu \(n^2\)là số chẵn thì n cũng là số chẵn
Giả sử n là số lẻ
Khi đó: n2 là số lẻ, trái với giả thiết
Vậy n là số chẵn.
Ta có n2 = n.n
mà n2 chẵn
=> n.n chẵn
=> n.n \(⋮\)2
=> có ít nhất 1 số chia hết cho 2
mà n = n => n \(⋮\)2 => n chẵn (đpcm)
Ta có : n^2 = n.n
Mà n^2 là chẵn .
=> n.n chẵn
=> n.n chia hết cho 2
Có ít nhất là 1 chữ số chia hết cho 2
Mà n = n => n chia hết chia hết cho 2
=> n chẵn ( đpcm )
chứng minh rằng ngoài 2 không có số chẵn nào là số nguyên tố
số chẵn là số chia hết cho 2
=> những số chẵn >2 đều có lớn hơn hoặc băng 3 ước đó là 1;2 và chính nó
vì mọi số chẵn đều chia hết cho 2 nên không có số nguyên tố nào là số chẵn ngoài 2
Chứng minh rằng : n . ( n + 1 ) là số chẵn với mọi số tự nhiên n
Nếu n là chẵn thì n+1 là lẻ.
Ta có: n.(n+1) là chẵn nhân lẻ nên sẽ có kết quả n.(n+1) là chẵn.
Nếu n là lẻ thì n+1 là chẵn
Ta có: n.(n+1) là lẻ nhân chẵn nên sẽ có kết quả n.(n+1) là chẵn
Vậy n . ( n + 1 ) là số chẵn với mọi số tự nhiên n
xet n=2k =>n chia het cho 2
xét n=2k+1=>n+1=2k+1+1=2k+2=2(k+1) chia hết cho 2
vay n.(n+1) la so chan voi moi so tu nhien n
Nếu n là chẵn thì n+1 là lẻ.
Ta có: n.(n+1) là chẵn nhân lẻ nên sẽ có kết quả n.(n+1) là chẵn.
Nếu n là lẻ thì n+1 là chẵn
Ta có: n.(n+1) là lẻ nhân chẵn nên sẽ có kết quả n.(n+1) là chẵn
Vậy n . ( n + 1 ) là số chẵn với mọi số tự nhiên n
Chứng minh rằng : n( n+7) là số tự nhiên chẵn với ọi số n
+ nếu n là số lẻ thì n + 7 là số chẵn => n(n + 7) là số chẵn
+ nếu n là số chẵn thì n(n + 7) là số chẵn
Vậy với mọi số n thì n(n + 7) là số chẵn
Sẽ có 2 trường hợp
TH1: n là số lẻ
n+7 sẽ bằng 1 số chẵn => n(n+7) là số tự nhiên chẵn
TH2: n là số chẵn
=>n(n+7) là số tự nhiên chẵn vì số chẵn nhân với số nào cũng được tích là 1 số chẵn
chứng minh rằng :n(n+2017) là số chẵn với mọi số tự nhiên n