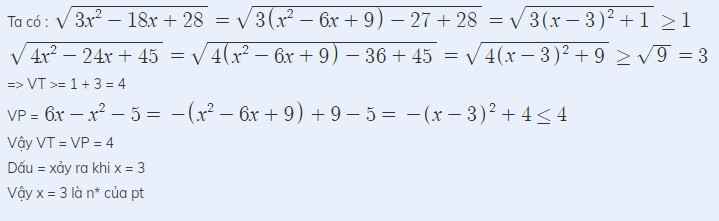giải phương trình: \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=5-x^2+6x\)

Những câu hỏi liên quan
Giải phương trình: \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-5-x^2+6x\)
giải phương trình :
a, \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
b, \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)
giải các phương trình sau :
a.\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
b. \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)
a) \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-x^2+6x-5\) (ĐKXĐ : \(1\le x\le5\) )\
Ta có : \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=\sqrt{3\left(x^2-6x+9\right)+1}+\sqrt{4\left(x^2-6x+9\right)+9}=\sqrt{3\left(x-3\right)^2+1}+\sqrt{4\left(x-3\right)^2+9}\)
\(\Rightarrow\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}\ge1+3=4\)
Lại có : \(-x^2+6x-5=-\left(x^2-6x+9\right)+4=-\left(x-3\right)^2+4\le4\)
Do đó, phương trình tương đương với : \(\begin{cases}1\le x\le5\\\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=4\\-x^2+6x-5=4\end{cases}\)\(\Rightarrow x=3\left(TM\right)\)
Vậy nghiệm của phương trình là x = 3
b) \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2+1}+\sqrt{\left(x-2\right)^2+4}+\sqrt{\left(x-2\right)^2+5}=3+\sqrt{5}\)
Mặt khác, ta có : \(\begin{cases}\sqrt{\left(x-2\right)^2+1}\ge1\\\sqrt{\left(x-2\right)^2+4}\ge2\\\sqrt{\left(x-2\right)^2+5}\ge\sqrt{5}\end{cases}\)\(\Rightarrow\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}\ge3+\sqrt{5}\)
Dấu đẳng thức xảy ra <=> x = 2.
Vậy nghiệm của phương trình : x = 2
Đúng 0
Bình luận (0)
giải phương trình:
\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=13-x^2+6x\)
Giải phương trình\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=\)
Viết tiếp đi.Không có kết quả là bao nhiêu thì làm sao giải được???
giải pt
a.\(2\sqrt{x-4}-\dfrac{1}{3}\sqrt{9x-36}=4-\sqrt{x-4}\)
b.\(3\sqrt{x-2}-\sqrt{x^2-4}=0\)
c.\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-5-x^2+6x\)
a,ĐK: x≥4
Ta có: \(2\sqrt{x-4}-\dfrac{1}{3}\sqrt{9x-36}=4-\sqrt{x-4}\)
\(\Leftrightarrow2\sqrt{x-4}-\sqrt{x-4}=4-\sqrt{x-4}\)
\(\Leftrightarrow2\sqrt{x-4}=4\)
\(\Leftrightarrow\sqrt{x-4}=2\Leftrightarrow x-4=4\Leftrightarrow x=8\left(tm\right)\)
Đúng 1
Bình luận (0)
b, ĐK: x≥2
Ta có: \(3\sqrt{x-2}-\sqrt{x^2-4}=0\)
\(\Leftrightarrow3\sqrt{x-2}-\sqrt{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(3-\sqrt{x+2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\3-\sqrt{x+2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x+2}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình:
a) \(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-x^2-5+6x\)
b) \(x+y+z+8=2\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\)
b/
\(pt\Leftrightarrow\left(x-1-2\sqrt{x-1}+1\right)+\left(y-2-4\sqrt{y-2}+4\right)+\left(z-3-6\sqrt{z-3}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2+\left(\sqrt{y-2}-2\right)^2+\left(\sqrt{z-3}-3\right)^2=0\)
\(\Leftrightarrow\sqrt{x-1}=1;\text{ }\sqrt{y-2}=2;\text{ }\sqrt{z-3}=3\)
\(\Leftrightarrow x=2;\text{ }y=6;\text{ }z=12\)
Đúng 0
Bình luận (0)
Tìm x : \(\text{ }\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-x^2+6x-5\)
Giải phương trình
\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-5-x^2+6\)
Mình fix luôn đề nhé.
Ta có :
+) \(\sqrt{3x^2-18x+28}=\sqrt{3\left(x^2-6x+9\right)+1}\)
\(=\sqrt{3\left(x-3\right)^2+1}\ge1\forall x\)
+) \(\sqrt{4x^2-24x+45}=\sqrt{4\left(x^2-6x+9\right)+9}\)
\(=\sqrt{3\left(x-3\right)^2+9}\ge\sqrt{9}=3\forall x\)
Do đó \(VT\ge4\forall x\)
Xét \(VP=-5-x^2+6x\)
\(=-\left(x^2-6x+5\right)\)
\(=-\left(x^2-6x+9-4\right)\)
\(=4-\left(x-3\right)^2\le4\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy pt có nghiệm duy nhất \(x=3\).
Đúng 0
Bình luận (1)
\(\sqrt{3x^2-18x+28}+\sqrt{4x^2-24x+45}=-5-x^2+6x\)
<=> \(\sqrt{3\left(x^2-6x+9\right)+1}+\sqrt{4\left(x^2-6x+9\right)+9}=4-\left(x^2-6x+9\right)\)
<=> \(\sqrt{3\left(x-3\right)^2+1}+\sqrt{4\left(x-3\right)^2+9}=4-\left(x-3\right)^2\)
Có \(\sqrt{3\left(x-3\right)^2+1}\ge\sqrt{0+1}=1\)
\(\sqrt{4\left(x-3\right)^2+9}\ge\sqrt{0+9}=3\)
=> VT=\(\sqrt{3\left(x-3\right)^2+1}+\sqrt{4\left(x-3\right)^2+9}\ge1+3=4\)
VP=\(4-\left(x-3\right)^2\le4\) với mọi x
=> Để VT=VP <=> \(x-3=0\) <=>x=3(t/m)
Vậy pt có nghiệm x=3
Đúng 0
Bình luận (0)