Cho đường thẳng x, B và C nằm ngoài đường thẳng x sao cho B và C không cùng một nửa mặt phẳng. Tìm M trên x sao cho MB/MC nhỏ nhất .

Những câu hỏi liên quan
Xét 2 điểm A và B trên cùng 1 nửa mặt phẳng bờ là đường thẳng a (Â,B không thuộc a). Gọi C là điểm nằm trên nửa mặt phẳng đối của nửa mặt phẳng trên sao cho đường thẳng a là đường trung trực của đoạn thẳng AC. Gọi M là điểm bất kì trên đường thẳng a, hãy so sánh MA + MB với BC. Khi nào MA + MB là nhỏ nhất?
Cho hai điểm A và B nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên đường thẳng d một điểm M sao cho tổng độ dài các đoạn thẳng MA+MB đạt giá trị nhỏ nhất
Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
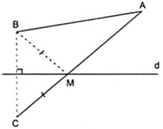
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d
Đúng 1
Bình luận (0)
Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
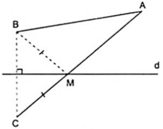
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d
Đúng 0
Bình luận (0)
a) Trên nửa mặt phẳng đối nhau có bờ là đường thẳng m, cho hai điểm A và B không thuộc đường thẳng m. Xác định vị trí điểm N sao cho NA + NB có giá trị bé nhất
b) Trên cùng một nửa mặt phẳng có bờ là đường thẳng n, cho 2 điểm phân biệt C, D không thuộc đường thẳng n. Xác định vị trí điểm M sao cho MC + MD có giá trị bé nhất
Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)
kkk em mới học lớp 7
em nói nhầm em mới học lớp 6
Cho đường thẳng đenta: x+y-3=0
a) A(1;-1) B(0;1) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
b) A(1;-1) B(2;3) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
Làm bừa coi xem đk :b
\(M\in\Delta:y=3-x\Rightarrow M\left(x;3-x\right)\)
a/ MA+MB min
\(MA=\sqrt{\left(x_A-x_M\right)^2+\left(y_A-y_M\right)^2};MB=\sqrt{\left(x_B-x_M\right)^2+\left(y_B-y_M\right)^2}\)
\(Minkovsky:MA+MB\ge\sqrt{\left(x_M-x_A+x_M-x_B\right)^2+\left(y_M-y_A+y_M-y_B\right)^2}\)
\("="\Leftrightarrow\dfrac{x_A-x_M}{y_A-y_M}=\dfrac{x_B-x_M}{y_B-y_M}\Leftrightarrow\dfrac{1-x}{-1-3+x}=\dfrac{-x}{1-3+x}\)
\(\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
|MA-MB| max
\(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{1+4}=\sqrt{5}\)
Theo bdt tam giác ta luôn có: \(\left|MA-MB\right|\le AB\)
\(\Leftrightarrow\left|\sqrt{\left(x_M-1\right)^2+\left(y_M+1\right)^2}-\sqrt{x_M^2+\left(y_M-1\right)^2}\right|\le\sqrt{5}\)
\("="\Leftrightarrow M,A,B-thang-hang\)
\(\Leftrightarrow\overrightarrow{MA}=k\overrightarrow{MB}\Leftrightarrow\left\{{}\begin{matrix}x_A-x_M=k\left(x_B-x_M\right)\\y_A-y_M=k\left(y_B-y_M\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1-x}{-x}=\dfrac{-4+x}{-2+x}\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
Câu b tương tự bạn tự làm nốt
Đúng 0
Bình luận (0)
Cho đường thẳng xy và hai điểm A, B nắm trên cùng một nửa mặt phẳng bờ là đường thẳng xy. Hãy tìm trên đường thẳng xy một điểm C sao cho chu vi tam giác ABC là nhỏ nhất?
Trên cùng nửa mặt phẳng bờ là đường thẳng xy lấy hai điểm A và B. Tìm điểm M trên đường thẳng xy sao cho MA + MB ngắn nhất.
Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x - 2y + 2 = 0 và A(0;6), B(2;5). Tìm tọa độ điểm M trên đường thẳng d sao cho MA + MB nhỏ nhất
Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Đúng 2
Bình luận (3)
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Đúng 2
Bình luận (0)














