Làm sao để biến đổi số thập phân thành phân số
1.786519669 = \(\frac{?}{?}\)
nêu công thức biến đổi
Biến đổi số thập phân thành phân số :
1.811576046 =\(?\)
và nêu công thức biến đổi .
Biến đổi mỗi biểu thức sau thành một phân thức đại số:
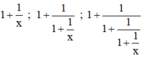
b) Em hãy dự đoán kết quả của phép biến đổi biểu thức:
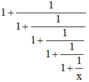
thành phân thức đại số và kiểm tra lại dự đoán đó.
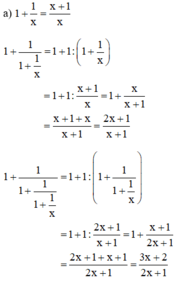
b) + Dự đoán :
Quy luật : Giả sử viết các phân thức trên thành một dãy thì phân thức sau có tử bằng tổng của tử và mẫu của phân thức đứng liền trước và mẫu bằng tử của phân thức đứng liền trước đó.
Do đó :
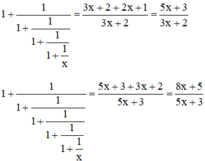
+ Kiểm chứng :
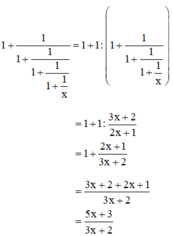
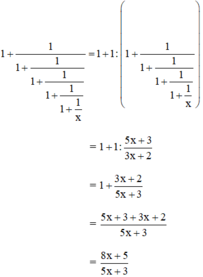
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
`a^2 + ab + 2a + 2b = a(a+2) + b(a+2) = (a+b)(a+2)`
Tìm phân số tối giản biến đổi được thành phân số thập phân có tích của tử và mẫu là 260
tìm phân số tối giản biến đổi được thành phân số thập phân có tích của tử và mẫu là 260
Biến đổi biểu thức sau thành phân thức đại số \(\frac{4+\frac{3}{x}}{5-\frac{3}{2x}}\)
Biến đổi tớ gọi B nhá cậu :)
\(B=\frac{\frac{3}{x}}{5-\frac{3}{2x}}=\frac{4x+3}{x}:\frac{10x-3}{2x}=\frac{4x+3}{x}.\frac{2x}{10x-3}=\frac{8x+6}{10x-3}\)
Bài này đơn giản làm theo dạng là được =))
tìm phân số tối giản biến đổi thành số thập phân có tích của tử và mẫu là 260
Biến đổi biểu thức sau thành một phân thức đại số:
\(\frac{x+\frac{1}{y}}{y+\frac{1}{x}}\)
\(\frac{x+\frac{1}{y}}{y+\frac{1}{x}}=\frac{\frac{xy}{y}}{\frac{xy}{x}}=\frac{xy}{y}.\frac{x}{xy}=\frac{x}{y}\)
\(\frac{x+\frac{1}{y}}{y+\frac{1}{x}}=\left(x+\frac{1}{y}\right):\left(y+\frac{1}{x}\right)=\frac{xy+1}{y}:\frac{xy+1}{x}=\frac{\left(xy+1\right)\cdot x}{\left(xy+1\right)\cdot y}=\frac{x}{y}\).
Chết mọe, lộn
\(=\frac{\frac{xy+1}{y}}{\frac{xy+1}{x}}=\frac{xy+1}{y}.\frac{x}{xy+1}=\frac{x}{y}\)
Dùng tính chất cơ bản của phân thức hoặc quy tắc đổi dấu để biến đổi mỗi cặp phân thức sau thành cặp phân thức bằng nó và có cùng mẫu thức: 4 x x + v à 3 x x - 1