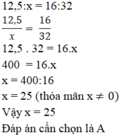Gía trị x < 0, thõa mãn: x4= 16

Những câu hỏi liên quan
Gía trị lớn nhất của x thõa mãn
\(^{x-1^{x+1}-x+1^{x+1}=0}\)
Gía trị của x thõa mãn: 2x+1/5 = 3y-2/7 = 2x+3y-1/6x
Gía trị nào dưới đây của x thỏa mãn 12,5 : x = 16 : 32 với x khác 0
A. x = 25
B. x = 5
C. x = 1 25
D. x = 35
Gía trị x thõa mãn:
| x-2,2|=|0,2-x|
nhanh nhé, k cần cách lm, chỉ cần đáp án
|x-2,2| =|0,2-x|<=> |x-2,2| -|0,2-x| = 0
|x-2,2|>=0
|0,2-x|>=0
mà |x-2,2|-|0,2-x| =0
hoặc =>x-2,2=0=> x =2
hoặc =>0,2-x=0=> x =0,2
Đúng 0
Bình luận (0)
Gía trị x<0 thỏa mãn:
x2= 16 phần 81
\(x^2=\frac{16}{81}\)
Vì \(x< 0\) nên \(x=-\sqrt{\frac{16}{81}}\)
\(\Rightarrow x=-\frac{4}{9}\)
Đúng 0
Bình luận (0)
Cho các số x,y,z thõa mãn \(x^2+2y+1=0;y^2+2z+1=0\) và \(z^2+2x+1=0\). Gía trị của biểu thức \(P=x^{2016}+y^{2016}+z^{2016}\)...
\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0+0+0\)
\(\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0\)
Mà \(\left(x+1\right)^2\ge0\)
\(\left(y+1\right)^2\ge0\)
\(\left(z+1\right)^2\ge0\)
\(\Rightarrow x+1=y+1=z+1=0\)
\(\Rightarrow x=y=z=-1\)
\(\Rightarrow P=1+1+1=3\)
Đúng 0
Bình luận (0)
Gía trị của x thõa mãn :
\(x\left(x-1\right)-\left(x+1\right)^2=4\)
x(x-1) -(x+1)^2 =4 <=> x^2 -x -(x^2 + 2x +1 )=4
<=> x^2 -x -x^2 -2x-1 =4
<=> -3x = 4+1
<=> -3x =5
<=>x=-5/3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Gía trị của x thõa mãn \(\frac{7x+2}{5x+7}=\frac{7x-1}{5x+1}\) là x = .....
Gía trị của x<0 thỏa mãn:
\(2x^4-31x^2-16=0\)