Cho 1 lục giác đều nội tiếp đường tròn . trên mỗi cạnh của lục giác ; ta dựng 1 hình tam giác sao cho 2 cạnh của tam giác không thuộc về phía đường tròn . Lấy tâm đường tròn ngoại tiếp của mỗi tam giác . Chứng minh : 6 điểm đó đồng quy với nhau và tạo thành 1 đường tròn

Những câu hỏi liên quan
Vẽ một lục giác đều ABCDEG nội tiếp đường tròn bán kính 2cm rồi vẽ hình 12 cạnh đều AIBJCKDLEMGN nội tiếp đường tròn đó.Nêu cách vẽ
*cách vẽ:
- vẽ đường tròn (O,2cm)
- Từ một điểm A trên đường tròn (O;2cm) đặt liên tiếp các cung bằng nhau có dây căng cung bằng 2cm
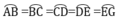
-Nối AB, BC, CD, DE, EG, GA ta được lục giác đều ABCDEG nội tiếp trong đường tròn (O;2cm)
-kẻ đường kính vuông góc với AB và DE cắt đường tròn lần lượt tại I và L. Ta có:
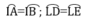
-kẻ đường kính vuông góc với BC và EG cắt đường tròn lần lượt tại J và M.Ta có:
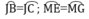
-kẻ đường kính vuông góc với CD và AG cắt đường tròn lần lượt tại N và K.Ta có:
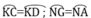
-Nối AI , IB, BJ, JC, CK, KD, DL, LE, EM, MG, GN, NA đa giác AIBJCKDLEMGN là đa giác đều mười hai cạnh nội tiếp trong đường tròn (O;2cm)
Đúng 0
Bình luận (0)
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
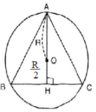
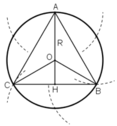
* Vẽ tam giác đều:
Chia đường tròn thành 6 cung bằng nhau như phần a).
Nối các điểm như hình vẽ ta được tam giác đều nội tiếp đường tròn.
* Tính cạnh tam giác :
Gọi cạnh ΔABC đều là a.
Gọi H là trung điểm BC
⇒ HB = a/2
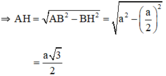
Tam giác ABC là tam giác đều có O là tâm đường tròn ngoại tiếp đồng thời là trọng tâm tam giác
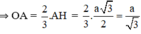
Mà OA = R ⇒ a = R√3.
Đúng 0
Bình luận (0)
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
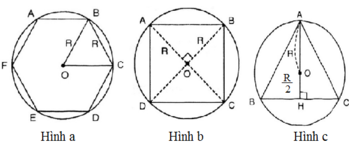
a)
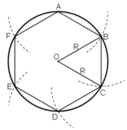
* Vẽ lục giác đều nội tiếp (O; R) :
+ Lấy điểm A trên (O ; R).
+ Vẽ cung tròn (A; R) cắt (O; R) tại B và F => AB = AF = R
+ Vẽ cung tròn (B; R) cắt (O; R) tại C ( khác A) => BC = R
+ Vẽ cung tròn (C; R) cắt (O; R) tại D ( khác B) => CD = R
+ Vẽ cung tròn (D; R) cắt (O; R) tại E ( khác C)=> DE = R
ABCDEF là lục giác đều cần vẽ.
* Tính cạnh: AB = BC = CD = DE = EF = FA = R.
b)
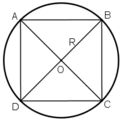
* Vẽ hình vuông :
+ Vẽ đường kính AC của đường tròn tâm O.
+ Vẽ đường kính BD ⊥ AC
Tứ giác ABCD có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.
Nối A với B ; B với C ; C với D với A ta được hình vuông ABCD nội tiếp đường tròn (O).
* Tính cạnh :
ΔAOB vuông tại O
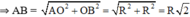
c)
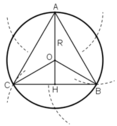
* Vẽ tam giác đều:
Chia đường tròn thành 6 cung bằng nhau như phần a).
Nối các điểm như hình vẽ ta được tam giác đều nội tiếp đường tròn.
* Tính cạnh tam giác :
Gọi cạnh ΔABC đều là a.
Gọi H là trung điểm BC
⇒ HB = a/2
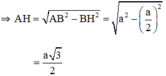
Tam giác ABC là tam giác đều có O là tâm đường tròn ngoại tiếp đồng thời là trọng tâm tam giác
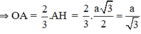
Mà OA = R ⇒ a = R√3.
Đúng 0
Bình luận (0)
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
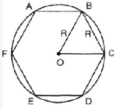
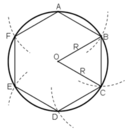
* Vẽ lục giác đều nội tiếp (O; R) :
+ Lấy điểm A trên (O ; R).
+ Vẽ cung tròn (A; R) cắt (O; R) tại B và F => AB = AF = R
+ Vẽ cung tròn (B; R) cắt (O; R) tại C ( khác A) => BC = R
+ Vẽ cung tròn (C; R) cắt (O; R) tại D ( khác B) => CD = R
+ Vẽ cung tròn (D; R) cắt (O; R) tại E ( khác C)=> DE = R
ABCDEF là lục giác đều cần vẽ.
* Tính cạnh: AB = BC = CD = DE = EF = FA = R.
Đúng 0
Bình luận (0)
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
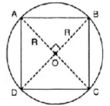
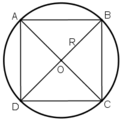
* Vẽ hình vuông :
+ Vẽ đường kính AC của đường tròn tâm O.
+ Vẽ đường kính BD ⊥ AC
Tứ giác ABCD có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.
Nối A với B ; B với C ; C với D với A ta được hình vuông ABCD nội tiếp đường tròn (O).
* Tính cạnh :
ΔAOB vuông tại O
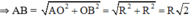
Đúng 0
Bình luận (0)
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
Hình a.
Gọi ai là cạnh của đa giác đều i cạnh.
a) a6= R (vì OA1A2 là tam giác đều)
Cách vẽ: vẽ đường tròn (O;R). Trên đường tròn ta đặt liên tiếp các cung ![]() ,
, ![]() ,...,
,..., ![]() mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
b) Hình b
Trong tam giác vuông OA1A2: a2 = R2 + R2 = 2R2 => a4 = R√2
Cách vẽ như ở bài tập 61.
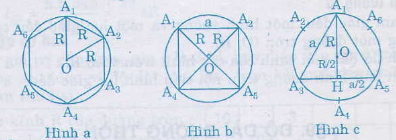
c) Hình c
A1H = R + =
A3H =
A1A3 = a
Trong tam giác vuông A1HA3 ta có: A1H2 = A1A32 – A3H2.
Từ đó = a2 -
.
=> a2 = 3R2 => a = R√3
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác A1A3A5 như trên hình c
Đúng 0
Bình luận (0)
Hình a.
Gọi ai là cạnh của đa giác đều i cạnh.
a) a6= R (vì OA1A2 là tam giác đều)
Cách vẽ: vẽ đường tròn (O;R). Trên đường tròn ta đặt liên tiếp các cung ![]() ,
, ![]() ,...,
,..., ![]() mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
b) Hình b
Trong tam giác vuông OA1A2: a2 = R2 + R2 = 2R2 => a4 = R√2
Cách vẽ như ở bài tập 61.

c) Hình c
A1H = R + =
A3H =
A1A3 = a
Trong tam giác vuông A1HA3 ta có: A1H2 = A1A32 – A3H2.
Từ đó = a2 -
.
=> a2 = 3R2 => a = R√3
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác A1A3A5 như trên hình c
Đúng 0
Bình luận (0)
Cho ABCDEF là lục giác lồi nội tiếp đường tròn bán kính R có các cạnh AB=CA=EF=R. Chứng minh rằng trung điểm 3 cạnh BC, DE, FA là đỉnh của một tam giác đều.
Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)
Giả sử lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE
Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm
Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)
Từ đó ta có :
\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{MP}\)
Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh
Đúng 0
Bình luận (0)
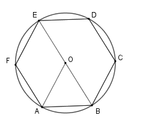
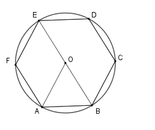
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O. Tính số đo góc AOB
A. 60 °
B. 120 °
C. 30 °
D. 240 °
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O. Tính số đo góc AOB
A. 60 °
B. 120 °
C. 30 °
D. 240 °