Biết: Tam giác ABC, góc B = 110 độ. Góc C = 30 độ. Ax là tia đối của tia AC. Tia phân giác của tam giác BAx cắt đoạn thẳng BC tại K.
Tìm: Chứng minh tam giác KAB có 2 góc bằng nhau.
Tam giác ABC có góc B = 110; góc C = 30 . Gọi Ax là tia đối AC. Tia phân giác của góc BAx cát đường thẳng BC tại K. Chứng minh rằng tam giác KAB có 2 góc bằng nhau.
Bài này ez mà bạn
Xét tam giác ABC có góc B = 110độ, góc C = 30độ => góc A = 180 - 110 - 30 = 40độ
=> góc BAx = 180 - 40 = 140độ ( kề bù )
=> góc KAB = 140độ : 2 = 70độ (1)
mặt khác ta có góc KBA = 180 - 110 = 70độ ( kè bù ) (2)
Từ (1)(2) => góc KAB = góc KBA ( đpcm )
Choo tam giác ABC có góc B bằng 120 độ góc C bằng 30 độ gọi Ax là tia đối của tia AC và phân giác của góc BAx cắt đường thẳng BC tại K. Chứng minh rằng tam giác KAB có 2 góc bằng nhau
Tam giác ABC có \(\widehat{B}=110^0,\widehat{C}=30^0\). Gọi Ax là tia đối của tia AC. Tia phân giác của góc BAx cắt đường thẳng BC tại K. Chứng minh rằng tam giác KAB có hai góc bằng nhau ?
Tam giác ABC có ∠B = 110o, ∠C = 30o. Gọi Ax là tia đối của tia AC. Tia phân giác của góc BAx cắt đường thẳng BC tại K. Chứng minh rằng tam giác KAB có hai góc bằng nhau.
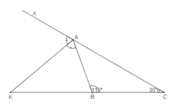
+) Hai góc ∠ABK và ∠ABC là hai góc kề bù nên:
∠ABK = 180° - ∠ABC = 180° - 110° = 70° (1)
+) Góc Bax là góc ngoài tam giác tại đỉnh A của tam giác ACK nên:
∠BAx = 110° + 30° = 140° ( tính chất góc ngoài tam giác).
+) Do AK là tia phân giác của góc BAx nên:
∠BAK = ∠BAx : 2 = 140° : 2 = 70°. (2)
Từ (1) và (2) suy ra tam giác KAB có hai góc bằng nhau.
tam giác ABC có góc ABC =110 độ , góc ACB = 30 độ . Kẻ tia Ax là tia đối của AC . Kẻ tia phân giác góc BAx cát đường thẳng BC ở D . chứng minh tam giác DAB cân
1. cho tam giác ABC có góc B= 110 độ, góc C= 30 độ. Gọi Ax là tia đối của tia Ac. Tia phân giác góc BAx cắt Bc tại K. Chứng minh rằng tam giác KAB có 2 góc bằng nhau
2. cho a, b,c là các số hữu tỉ khác 0 sao cho a+b-c/c = a-b+c/b = -a+b+c/a . Tính giá trị bằng số của một biểu thức M = (a+b)(b+c)(c+a)/abc
giúp mình với nhé
1. Tính góc B và góc C của tam giác ABC biết:
a, Góc A= 70*, góc B - góc C=10*
B, Góc A= 60*, góc B-góc C =2gocC
2.Tính các góc của tam giác ABC. Biết góc A: góc B: góc C=2:3:4
3. Cho góc xOy; điểm A thuộc tia Ox. Kẻ AB vuông góc với Ox (B thuộc Oy). Kẻ BC thuộc Oy (C thuộc Oy). Kẻ CD vuông góc với Ox (D thuộc Oy).
a, Tìm các tam giác vuông trong hình vẽ
b, Tìm góc = góc AOB
4. Cho tam giác ABC có góc B = 110*, góc C= 30*. Gọi Ax là tia đối của tia AC. Tia phân giác của góc BAx cắt đường thẳng BC tại K. Chứng minh tam giác KAB có 2 góc bằng nhau.
1. Cho tam giác ABC, góc A = 120 độ, đường phân giác AD. Đường phân giác góc ngoài tại C cắt đường thẳng AB ở K. Gọi E là giao điểm của DK và AC. Tính số đo của góc BED.
2. Cho tam giác ABC có BC = 17cm, CA = 15cm, AB = 8cm. Ba đường phân giác của tam giác cắt nhau tại O. Tính tổng các khoảng cách từ O đến ba cạnh của tam giác.
3. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Gọi D là điểm thuộc đoạn MC, H là hình chiếu của B trên AD. Chứng minh HM là tia phân giác của góc BHD.
4. Cho tam giác ABC và điểm I là giao điểm 3 đường phân giác của tam giác. Gọi H là chân đường vuông góc kẻ từ B đến AI. Chứng minh rằng góc IBH = góc ICA.
5. Cho tam giác ABC có góc B = 50 độ, góc C = 20 độ, đường cao AH. Tia phân giác của góc AHC cắt AC tại D. Vẽ tia Ax là tia đối của tia AB. Chứng minh điểm D nằm trên tia phân giác của góc ABC.
1. Cho tam giác MNP có góc M = 40 độ, góc N = 100 độ. Chứng minh tam giác MNP là tam giác cân.
2. Cho tam giác ABC có góc A = 80 độ, góc B = 50 độ. Đường thẳng song song với BC cắt tia đối của tia AB tại D và cắt tia đối của tia AC tại E. Chứng minh rằng tam giác ADE là tam giác cân
Bài 1:
Tam giác MNP có: \(\widehat{M}=40^o;\widehat{N}=100^o\)
Tổng số đo 3 góc của 1 tam giác là 180o, ta được:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\\ \Leftrightarrow40^o+100^o+\widehat{P}=180^o\\ \Leftrightarrow140^o+\widehat{P}=180^o\\ \Leftrightarrow\widehat{P}=180^o-140^o=40^o\)
Vì: \(\widehat{M}=\widehat{P}=40^o\) => Tam giác MNP là tam giác cân tại N (ĐPCM)