cho tam giác ABC vuông tại A . Kẻ AH vuông góc vs BC ( H thuộc BC ) . B iết HB = 9cm , HC = 16cm . tính độ dài AH
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC).Biết HB = 9cm, HC = 16cm. Tính độ dài AH.
Cho tam giac ABC vuông tại A. Kẻ AH vuông góc với BC(H thuộc BC). Biết HB = 9cm, HC = 16cm. Tính độ dài AH?
AH = 12. đúng 100%. mình giải rùi
Đúng 0
Bình luận (0)
Bạn tự vẽ hình ra hì. Mình vẽ ko được
Bài làm
Tam giác AHB vuông tại H: AH^2+HB^2=AB^2
Tam giác AHC vuông tại H:AH^2+HC^2=AC^2
Tam giác ABC vuông tại A:BC^2=AB^2+AC^2
BC=HB+HC=9+16=25
BC^2=AH^2+HB^2+AH^2+HC^2=2AH^2+HB^2+HC^2=25^2=625
2HA^2+9^2+16^2=625
2HA^2+337=625
2HA^2=288
HA^2=144
HA=12
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ đường cao AH (H thuộc cạnh BC). Biết HB = 9cm, HC = 16cm. Tính độ dài: AH, AB.
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Biết HB = 9cm; HC = 16cm. Tính AH.
Help me
Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng hệ thức : AH^2 = HB . HC = 16 . 9
=> AH = 4 . 3 = 12 cm
Đúng 3
Bình luận (0)
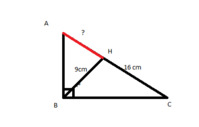
Áp dụng hệ thức liên quan tới đường cao vào Δvuông ABC, ta được:
AH²= BH.CH = 9.16 = 144
⇒ AH=12 (cm)
Đúng 2
Bình luận (0)
câu 1 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC. Biết AB = 20cm, BH = 16cm, HC = 5cm. Tính AH, AC.
câu 2 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC, biết AC = 15cm, HB = 5cm, HC = 9cm . Tính độ dài cạnh AB.
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, trên cạnh BC, lấy điểm M, sao cho BM=BA. Kẻ AH vuông góc vs BC tại H, MI vuông góc vs AC tại I.
1, chứng minh góc BAM= góc BMA
2, chứng minh AM là tia phân giác của góc HAC
3, chứng minh AI=AH và AB+AC<BC+AH
4, khi AH=12cm, HB=9cm, HC=16cm
a, tính độ dài AB và AC
b, chứng minh góc B>góc C
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC( H thuộc BC). Tính độ dài AH biết HB=2 cm, HC=8 cm
cho tam giác abc có ah vuông góc bc tại h . có hb=9cm ,hc=16cm ,
Tính ab ,ac,bc
Áp dụng hệ thức lượng giác vào tam giác vuông ABC có:
(AH vuông góc với BC): \(\Rightarrow AH^2=BH\cdot CH=9\cdot16=144\Rightarrow AH=12cm\)
\(\Rightarrow BC=BH+CH=9+16=25cm\)
Áp dụng định lí Pytago vào các tam giác vuông có:
Tam giác vuông \(AHB\) có: \(AB^2=AH^2+BH^2=12^2+9^2=225\Rightarrow AB=15cm\)
Tam giác vuông AHC có: \(AC^2=AH^2+CH^2=16^2+12^2=400\Rightarrow AC=20cm\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A(H thuộc BC). HB=9cm, HC=16cm. Tính AH?
BC=9+16=25(cm)
tam giác AHB_|_ tại H
áp dụng định lí py-ta-go, ta có:
\(AH^2=AB^2-HB^2=AB^2-9^2=AB^2-81\left(1\right)\)
tam giác AHC vuông tại H
\(\Rightarrow AH^2=AC^2-CH^2=AC^2-16^2=AC^2-256\left(2\right)\)
từ (1)(2) suy ra :\(AH^2+AH^2=AB^2-81+AC^2-256\)
\(\Rightarrow2.AH^2=\left(AB^2+AC^2\right)-81-256\)
\(\Rightarrow2.AH^2=BC^2-337\)( vì tam giác ABC vuông tại A nên AB^2+AC^2=BC^2)
\(\Rightarrow2.AH^2=25^2-337=625-337=288\)
\(\Rightarrow AH^2=288:2=144\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)
Đúng 0
Bình luận (0)
thiếu đề kìa, phần thiếu là kẻ AH_|_BC tại H ak
Đúng 0
Bình luận (0)