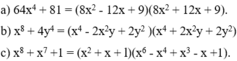Phân tích thành nhân tử Nhân tử : x4y4+64

Những câu hỏi liên quan
phân tích đa thức x4+64 thành nhân tử
Ta có:
x^4 + 64 = (x²)² + 8² + 2x².8 - 2.x².8
= (x² + 8)² - (4x)²
= (x² - 4x + 8)(x² + 4x + 8)
Đúng 0
Bình luận (0)
Ta có:
x^4 + 64 = (x²)² + 8² + 2x².8 - 2.x².8
= (x² + 8)² - (4x)²
= (x² - 4x + 8)(x² + 4x + 8)
Đúng 0
Bình luận (0)
phân tích thành nhân tử
x4 + 64
phân tích đa thức thành nhân tử : -16x2+64
a) x3 + 2x2y + xy2 – 9x
(Có x là nhân tử chung)
= x(x2 + 2xy + y2 – 9)
(Có x2 + 2xy + y2 là hằng đẳng thức)
= x[(x2 + 2xy + y2) – 9]
= x[(x + y)2 – 32]
(Xuất hiện hằng đẳng thức (3)]
Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức: x3+64
Phân tích đa thức thành nhân tử
x4+64
Ta có:
x^4 + 64 = (x²)² + 8² + 2x².8 - 2.x².8
= (x² + 8)² - (4x)²
= (x² - 4x + 8)(x² + 4x + 8)
k nhoa
Đúng 1
Bình luận (0)
Ta có:
x^4 + 64 = (x²)² + 8² + 2x².8 - 2.x².8
= (x² + 8)² - (4x)²
= (x² - 4x + 8)(x² + 4x + 8)
k nhoa
Đúng 1
Bình luận (0)
\(x^4+64=\left(x^2\right)^2+8^2=\left(x^2+8\right)\left(x^2-8\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
\(x^4+64\)Phân tích đa thức thành nhân tử
hdt thức nha bạn
~~~~~~~~~~~~~
^_^
Đúng 0
Bình luận (0)
\(x^4+64\)
\(=\left(x^2\right)^2+8^2+2x^2.8-2x^2.8\)
\(=\left(x^2+8\right)^2-\left(4x^2\right)\)
\(=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\)
Đúng 0
Bình luận (0)
\(x^4+64\)
\(=\left(x^4+16x^2+64\right)-16x^2\)
\(=\left(x^2+8\right)^2-\left(4x\right)^2\)
\(=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử:a) 64
x
4
+ 81; b)
x
8
+
4
y
4
; c)
x
8
+
x
7
+1.
Đọc tiếp
Phân tích đa thức thành nhân tử bằng phương pháp thêm bớt hạng tử:
a) 64 x 4 + 81; b) x 8 + 4 y 4 ; c) x 8 + x 7 +1.
phân tích đa thức đa thức thành nhân tử : X4 + 64
x4 + 64 = (x4 + 16x2 + 64) - 16x2 = (x2 + 8)2 - (4x)2 = (x2 - 4x + 8).(x2 + 4x + 8)
Đúng 0
Bình luận (0)
Ta có
x4 + 64
= (x4 + 16x2 + 64) - 16x2
= (x2 + 8)2 - (4x)2
= (x2 - 4x + 8).(x2 + 4x + 8)
hok tốt
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử : \(x^3-64\)
Ta có : \(x^3-64\)
\(=x^3-4^3\)
Áp dung hằng dẳng thức : \(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(\Rightarrow x^3-4^3=\left(x-4\right)\left(x^2+4x+4^2\right)\)
Đúng 0
Bình luận (0)
\(x^3\)\(-64\)\(=x^3\)\(-4^3\)=\(\left(x-4\right)\)\(\left(x^2+4x+16\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời