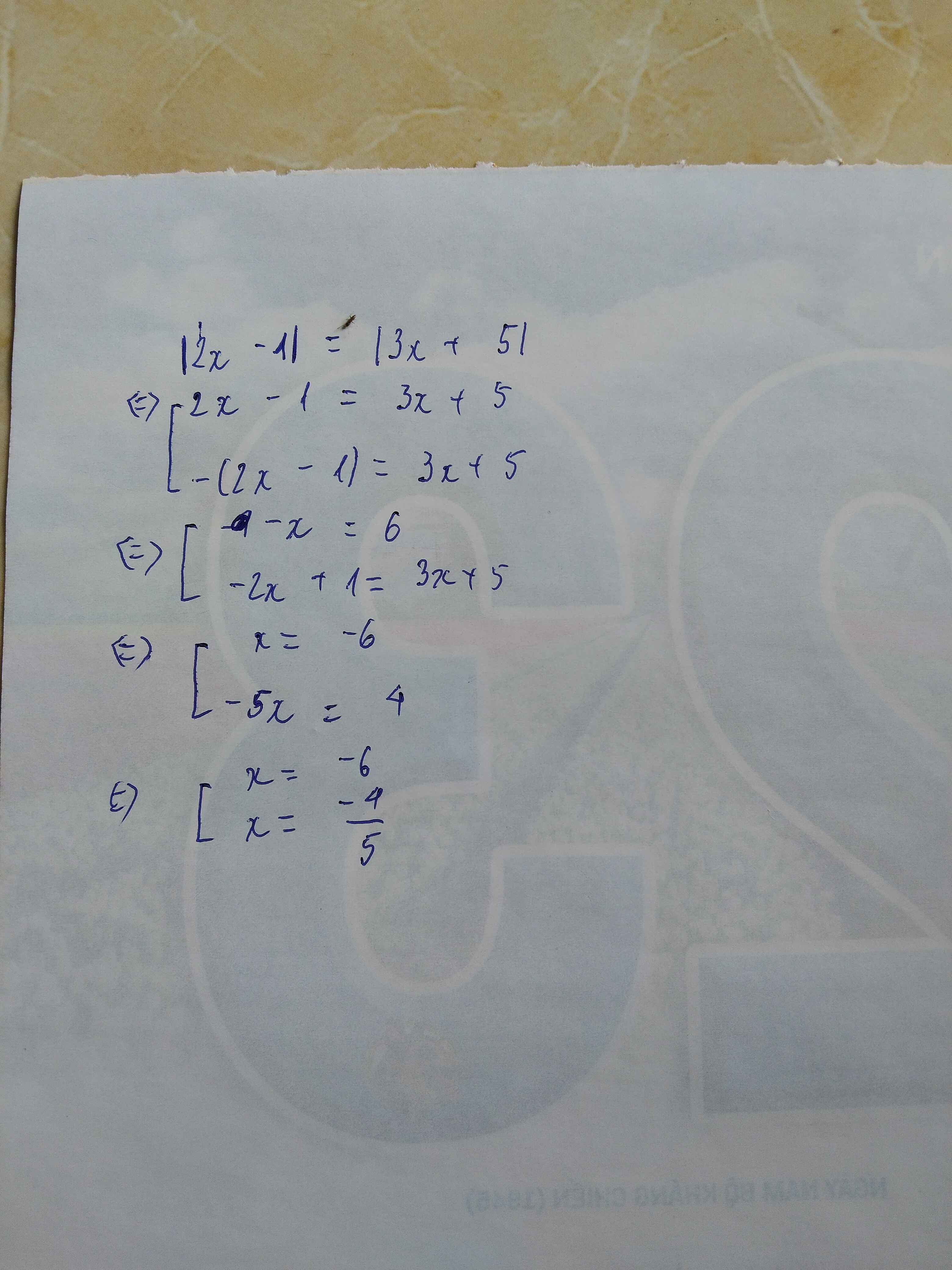Ta có \(\hept{\begin{cases}\left|3x-5\right|\ge0\forall x\\\left|2x-y\right|\ge0\forall y\end{cases}}\Leftrightarrow\left|3x-5\right|+\left|2x-y\right|\ge0\forall x;y\)

Dấu "=" xảy ra <=> \(\hept{\begin{cases}3x-5=0\\2x-y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=\frac{10}{3}\end{cases}}\)

Vậy x = 5/3 ; y = 10/3 là giá trị cần tìm 

\(a)\left|2x-5\right|=4\)\(\Rightarrow2x-5=\pm4\)

\(Với\)\(2x-5=4\Rightarrow2x=9\Rightarrow x=\frac{9}{2}\)

\(Với\)\(2x-5=-4\Rightarrow2x=1\Rightarrow x=\frac{1}{2}\)

\(Vậy\)\(x=\frac{9}{2};x=\frac{1}{2}\)

\(b)\left|2x-3\right|-\left|3x+2\right|=0\)

\(Vì\)\(\left|2x-3\right|\ge0;\left|3x+2\right|\ge0\)

\(\Rightarrow\hept{\begin{cases}2x-3=0\\3x+2=0\end{cases}\Rightarrow\hept{\begin{cases}2x=3\\3x=-2\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{3}{2}\\x=\frac{-2}{3}\end{cases}}}\)

\(Vậy\)\(x=\frac{3}{2};x=\frac{-2}{3}\)

 A = { \(\phi\)}

a, \(\left|2x-5\right|=4\)

\(\Rightarrow\orbr{\begin{cases}2x-5=4\\2x-5=-4\end{cases}\Rightarrow}\orbr{\begin{cases}2x=9\\2x=1\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{9}{2}\\x=\frac{1}{2}\end{cases}}\)

b, \(\left|2x-3\right|-\left|3x+2\right|=0\)

\(\Rightarrow\left|2x-3\right|=\left|3x+2\right|\)

\(\Rightarrow\orbr{\begin{cases}2x-3=3x+2\\2x-3=-3x-2\end{cases}\Rightarrow}\orbr{\begin{cases}-x=5\\5x=1\end{cases}\Rightarrow}\orbr{\begin{cases}x=-5\\x=\frac{1}{5}\end{cases}}\)

c, \(\left|x+3\right|-\left|3x+2\right|=x+2\)

Ta có: x + 3 = 0 => x = -3

           3x + 2 = 0 => x = -2/3

Lập bảng xét dấu: 

Với x < -3

Ta có: -x - 3 + 3x + 2 = x + 2

<=> 2x - 1 = x + 2

<=> x = 3 ( ko t/mãn )

Với -3 ≤ x < -2/3

Ta có: x + 3 + 3x + 2 = x + 2

<=> 4x + 5 = x + 2

<=> 3x = -3

<=> x = -1 ( t/mãn )

Với -2/3 ≤ x 

Ta có: x + 3 - 3x - 2 = x + 2

<=> -2x + 1 = x + 2

<=> -3x = 1

<=> x = -1/3 ( t/mãn )

Vậy....

d, \(\left||x-1|-5\right|=x+5\)

Đk: x + 5 ≥ 0 => x ≥ -5

\(\Rightarrow\orbr{\begin{cases}\left|x-1\right|-5=x+5\\\left|x-1\right|-5=-x-5\end{cases}\Rightarrow\orbr{\begin{cases}\left|x-1\right|=x+25\\\left|x-1\right|=-x\left(Loai\right)\end{cases}}}\)

Giải \(\left|x-1\right|=x+25\)

\(\Rightarrow\orbr{\begin{cases}x-1=-x-25\\x-1=x+25\end{cases}\Rightarrow\orbr{\begin{cases}2x=-24\\0x=26\left(Loai\right)\end{cases}\Rightarrow x}=-12}\)( ko t/mãn )

Vậy x \(\in\varnothing\)

\(\left|2x-1\right|=\left|3x+5\right|\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3x+5\\2x-1=-3x-5\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=-\dfrac{4}{5}\end{matrix}\right.\)

\(x=\frac{a}{b};a,b>0;\left(a,b\right)=1\).

\(\frac{5}{x}=\frac{5b}{a}\inℤ\Rightarrow a\inƯ\left(5\right)=\left\{1,5\right\}\).(vì \(\left(a,b\right)=1\))

Với \(a=1\):

\(2x=\frac{2}{b}\inℤ\Rightarrow b\inƯ\left(2\right)=\left\{1,2\right\}\)

Thử lại \(x=1,x=\frac{1}{2}\)đều thỏa mãn. 

Với \(a=5\):

\(2x=\frac{10}{b}\Rightarrow b\inƯ\left(10\right)=\left\{1,2,5,10\right\}\)

\(\left(a,b\right)=1\)nên \(b\in\left\{1,2\right\}\).

Thử lại \(x=5,x=\frac{5}{2}\)đều thỏa mãn. 

Vậy \(x\in\left\{1,\frac{1}{2},5,\frac{5}{2}\right\}\).

2x và 5/x 

2x luôn là số nguyên 

Vậy để thỏa đề thì 5/x phải là số nguyên 

=> 5 chia hết cho x 

x thuộc ước của 5 

mà x > 0 

Vậy x = 1 hoặc x = 5