BC=8 => CO=4 (O là trung điểm)

xét tam giác vuông COH có góc O bằng 30 độ => CH =1/2OC=2

=> SABDC=2SACD=2.1/2.2.8=16 (cm2) 

Chọn C

Gọi O là giao điểm của hai đường chéo AC và BD.

AC = BD (tính chất hình chữ nhật)

\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)

\(AD=\dfrac{1}{2}AC\left(gt\right)\)

\(\Rightarrow OA=OD=AD\)

\(\Rightarrow\Delta OAD\) đều

\(\Rightarrow\widehat{AOD}=60^0\)

60 độ bạn nhé, có cần mk giả chi tiết ko?

Xét tam giác vuông ACD vuông tại A có AD=AC/2 => ACD=30 độ => ADC=60 độ

Gọi giao điểm 2 đường chéo của hcn là O => OA=OD => tam giác AOD cân tại O mà ADC = 60 độ => tam giác AOD đều => AOD=60 độ :)

dễ thế đáp án bằng 60 . tick mình nhé .chúc bạn học tốt

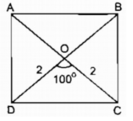
* Cách dựng:

- Dựng ∆ OAB biết OA = OB = 2cm, ∠ (AOB ) = 100 0

- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm

- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm

Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng

* Chứng minh:

Ta có: OA = OC, OB = OD

Suy ra tứ giác ABCD là hình bình hành.

Vì AC = BD = 4 (cm) nên hình bình hành ABCD là hình chữ nhật.

Gọi giao điểm của hai đường chéo là \(O\) .

Theo bài ra thì \(\widehat{AOD}=30^o\)

Theo tính chât hình chữ nhật thì \(OA=OD\) ( cùng bằng nửa độ dài đường chéo )
\(\Rightarrow\Delta OAD\) cân tại O

\(\Rightarrow\widehat{CAD}=\widehat{OAD}=\frac{180^o-\widehat{AOD}}{2}=\frac{180^o-30^o}{2}=75^o\)

Xét tam giác vuông tại D là DAC :
\(\frac{AD}{AC}=cos\widehat{CAD}\Rightarrow AD=cos\widehat{CAD}.AC=cos75^o.4\)

\(\frac{DC}{AC}=sin\widehat{CAD}\Rightarrow DC=ACsin\widehat{CAD}=4sin75^o\)

Do đó diện tích ABCD là :

\(AD.DC=4cos75^o.4sin75^o=4\left(cm^2\right)\)