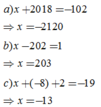Tìm 2 số dương khác nhau x;y biết rang : Tổng;hiệu và tích của chúng lần lượt tỉ lệ nghịch với 35;210 và 12

Những câu hỏi liên quan
tìm 2 số dương khác nhau x,y biết :tổng ,hiệu, tích của chúng tỉ lệ nghịch với 35,210,12
Theo đề bài ta có: \(35\left(x+y\right)=210\left(x-y\right)=12xy\)
\(\Rightarrow\frac{35\left(x+y\right)}{420}=\frac{210\left(x-y\right)}{420}=\frac{12xy}{420}\)
\(\Rightarrow\frac{x+y}{12}=\frac{x-y}{2}=\frac{xy}{35}\left(1\right)\)
Áp dụng TCDTSBN ta có:
\(\frac{x+y}{12}=\frac{x-y}{2}=\frac{\left(x+y\right)+\left(x-y\right)}{12+2}=\frac{2x}{14}=\frac{x}{7}\left(2\right)\)
\(\frac{x+y}{12}=\frac{x-y}{2}=\frac{\left(x+y\right)-\left(x-y\right)}{12-2}=\frac{2y}{10}=\frac{y}{5}\left(3\right)\)
Từ (1) và (2) => \(\frac{xy}{35}=\frac{x}{7}\Rightarrow\frac{xy}{35}=\frac{xy}{7y}\Rightarrow y=5\)
Từ (1) và (3) => \(\frac{xy}{35}=\frac{y}{5}\Rightarrow\frac{xy}{35}=\frac{xy}{5x}\Rightarrow x=7\)
Đúng 0
Bình luận (0)
tìm 3 số nguyên dương x;y;z đôi 1 khác nhau thỏa mãn x^3+y^3+z^3=(x+y+z)^2
Tìm các số nguyên dương x.y khác nhau sao cho: x^y=y^x
Tìm bộ số nguyên dương khác nhau (x; y; z) sao cho x2 + y - z =100 và x + y2 -z = 124
tìm số nguyên dương x,y khác nhau sao cho: Xy=yx
Tìm số nguyên x, biết:
a) x+2018 là số nguyên âm lớn nhất có ba chữ số khác nhau.
b) x-202 là số nguyên dương nhỏ nhất.
c) Tổng của ba số x; -8; 2 bằng -19.
tìm các số nguyên dương x, y khác nhau sao cho xy=yx
Tìm các số nguyên dương khác nhau x và y thỏa mãn x^3+7y=y^3+7x
Tìm 2 số dương khác nhau x;y biết rang : Tổng;hiệu và tích của chúng lần lượt tỉ lệ nghịch với 35;210 và 12
Ta có: 35(x+y)=210(x-y)=12xy
Suy ra: x+y/12=x-y/2=xy/35
Áp dụng tính chất dãy tỉ số bằng nhau ta có
x+y/12=x-y/2=(x+y)+(x-y)/12+2=(x+y)-(x-y)/12-2=x/7=y/5
Ta lại có:
x/7=y/5=xy/35
xy/35=x/7
y=5
Suy ra: x=7
Đúng 0
Bình luận (0)
bn tuyên sai rồi tỉ lệ nói ko nghĩa là tỉ lệ thuận lúc đầu phải là \(\frac{x+y}{35}=\frac{x-y}{210}=\frac{xy}{12}\)rồi ms làm tiếp
ai thấy đúng tk nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời