cho hình thang vuông MNPQ. MN =1/3 PQ. QN cắt PN tại O. Kéo dài QM và PN và PM, cắt nhau tại K.
a) So sánh diện tích hình MOQ và diện tích hình NOP
b) diện tích hình MNPQ = 180cm2
diện tích hình KMN = ?
c) so sánh KM và MQ
Những câu hỏi liên quan
cho hình thang vuông MNPQ vuông góc tại M và Q ; MN = 1/3 PQ . kéo dài QM vàPN cắt nhau tại K
A, so sánh diện tích 2 tam giác MNP và MQP
B,so sánh diện tích 2 tam giác MNK và MPK
C, diện tích hình thang MNPQ bằng 128 cm2 tính diện tích tam giác KNM
A, vi hai tam giác MNP&MQP có chung chiều cao và MN=1/3PQ nên
Suy ra Tam giác MNP=1/3tam giác MQP
Đúng 0
Bình luận (0)
Cho hình thang vuông MNPQ vuông góc tại M và Q ; PQ = 1/2 MN. Kéo dài MQ và NP cắt nhau tại A .a) So sánh diện tích hai tam giác MNP và MQP.
b) So sánh diện tích hai tam giác AQP và AQN
c) diện tích hình thang MNPQ bằng 63cm2.TÍnh diện tích tam giác AQP
Cho hình thang MNPQ Đáy MN=1/2 đáy PQ 2 đường chéo MP và NQ cắt nhau tại O
a,So sánh diện tích tam giác MNP và MPQ
b,Hãy chứng tỏ diện tích tam giác MOQ=NOP
Bài 1
Cho hình thang MNPQ
Đáy MN=1/2 đáy PQ
2 đường chéo MP và NQ cắt nhau tại O
a,So sánh diện tích tam giác MNP và MPQ
b,Hãy chứng tỏ diện tích tam giác MOQ=NOP
Moi người vẽ hình làm công thức lớp 5 nhé
Cho hình thang MNPQ, có đáy bé MN bằng 3/5 đáy lớn PQ. Hai đường chéo MP và NQ cắt nhau tại K. Biết diện tích tam giác NPK là 15cm2. Tính diện tích hình thang MNPQ.
Lời giải:
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)
Đúng 3
Bình luận (0)
cho hình thang MNPQ đáy MN =1/2 đáy PQ 2 đường chéo MP và NQ cắt nhau tại O a.So sánh diện tích tam giác MNP và MNQ b.Hãy chính tỏ diên tích tam giác MOQ = NOP
giúp mik với đang gấp lắm!
Cho hình thang vuông ABCD vuông tại A và D.Đáy AB = 1/3 CD.2 Đường chéo cắt nhau tại I.
a,So sánh diện tích ADC và diện tích ABD
b,Chứng Minh diện tích AID=diện tích BIC
c,Kéo dài 2 cạnh bên của hình thang cắt nhau tại K.So sánh KB - BC
a/ Sadc = 3 Sabd
b/ Sadc=Sabd vì Sacd= Sdbc
c/ bc=2 kb
Cho hình thang MNPQ có đáy bé MN bằng 6cm, có đáy lớn QP bằng 14 cm, MP cắt NQ tại O, biết diện tích tam giác MOQ bằng 36cm2. Tính:
a) Diện tích tam giác NOP
b) Tỉ số diện tích tam giác MOQ và diện tích tam giác OQP
Xem chi tiết
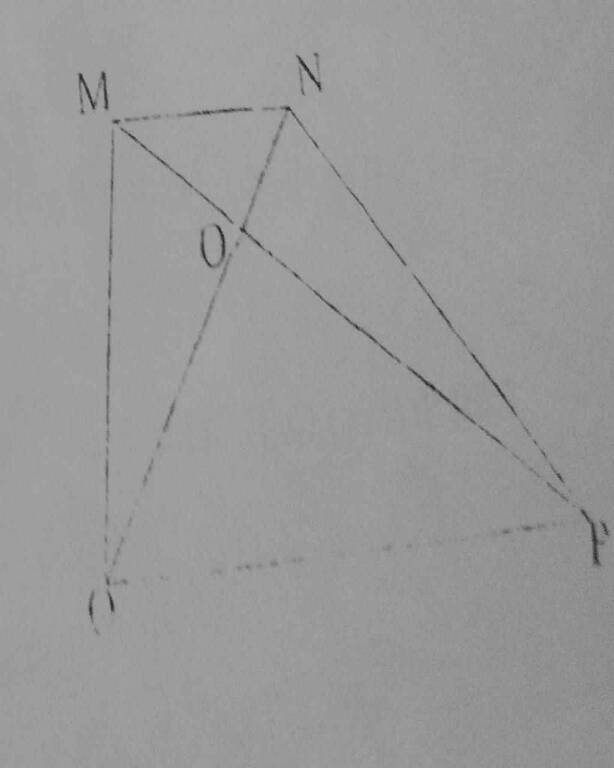b) Tỉ số diện tích tam giác MOQ và diện tích tam giác OQP
cho hình thang MNPQ có đáy MN =6cm,PQ=9cm.Hai đường chéo MP,NQ cắt nhau tại I.Biết diện tích NIP =12cm².Tính diện tích MNPQ