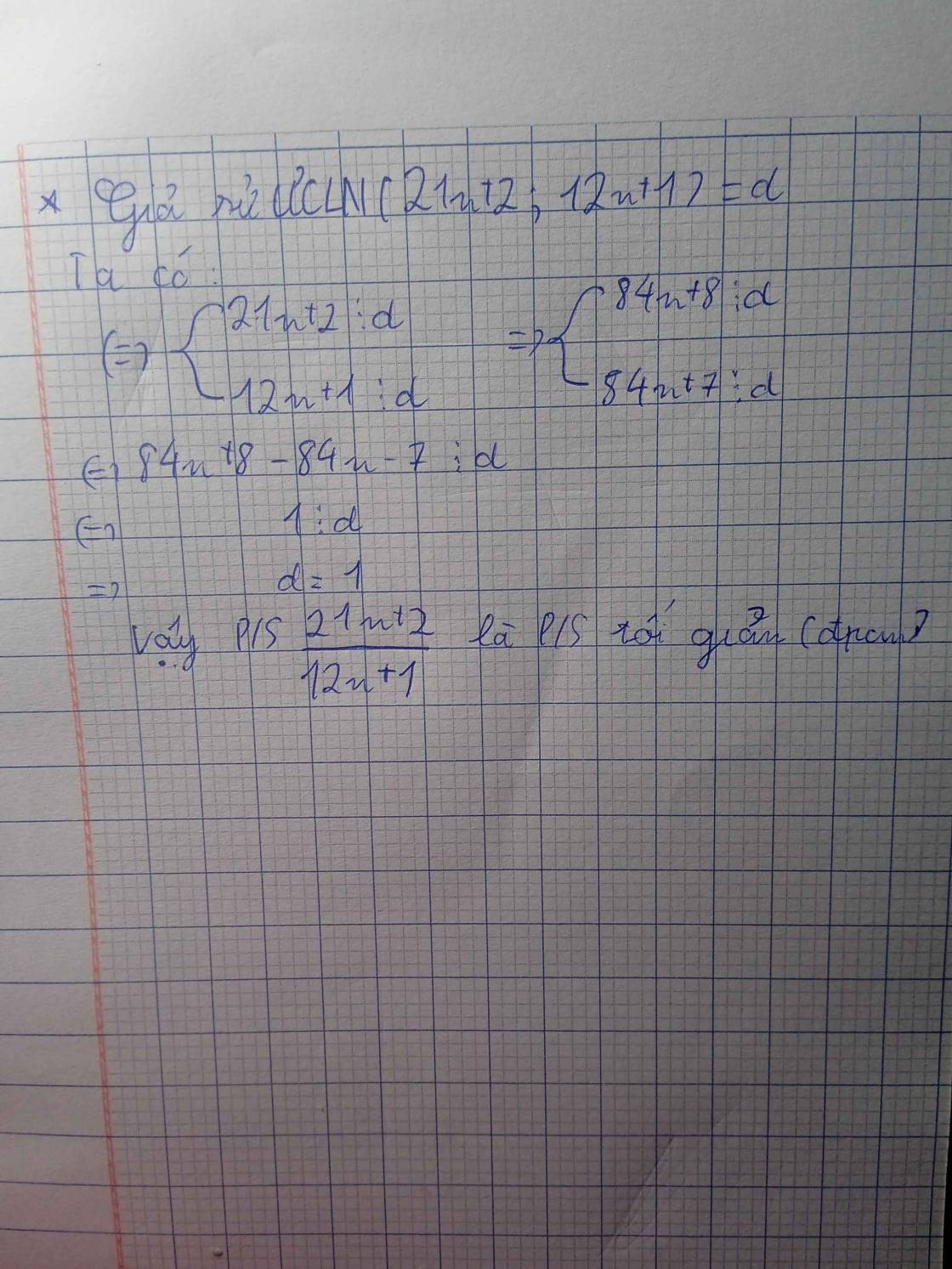chứng minh rằng với mọi n thuộc N phân số 21n+1^ 18n+1 là phân số tối giản

Những câu hỏi liên quan
a, Tìm phân số a/b biết a/b = 21/35 và ƯCLN(a;b) =30
b, Chứng minh rằng các phân số sau là phân số tối giản với mọi n thuộc N
1, 14n+3/21n+4 2,8n+3/18n+3
c, Chứng tỏ rằng phân số (n+1)(n+2)(n+3)....(n+n)/2^n
Với mọi n thuộc N chứng minh các phân số sau tối giản :
n+22 / n+3
3n+2/2n+3
18n+3/21n+7
a, Tìm phân số a/b biết a/b = 21/35 và ƯCLN(a;b) =30
b, Chứng minh rằng các phân số sau là phân số tối giản với mọi n thuộc N
1, 14n+3/21n+4 2,8n+3/18n+3
c, Chứng tỏ rằng phân số (n+1)(n+2)(n+3)....(n+n)/2^n
Chứng minh rằng: 21n+1 / 14n+3 là phân số tối giản với mọi số tự nhiên n.
dạ em chào anh ghi cái gì mà tui ko hỉu gì hết
Đúng 0
Bình luận (0)
bài 4 chứng minh rằng cá phân số sau đây tối giản với mọi n thuộc Z
a) 21n = 4 phần 14n + 3
b)21n + 1 phần 2n ( n = 1)
Chứng minh rằng phân số dfrac{21n+4}{14n+3} là phân số tối giản với mọi số tự nhiên n.
Đọc tiếp
Chứng minh rằng phân số \(\dfrac{21n+4}{14n+3}\) là phân số tối giản với mọi số tự nhiên
Gọi \(\text{ƯCLN(21n+4,14n+3)}\) là \(\text{d}\)
\(\Rightarrow\) \(\text{21n+4 ⋮ d}\)
\(\text{14n+3 ⋮ d}\)
\(\Rightarrow\) \(\text{[3(14n+3)-2(21n+4) ⋮ d}\)
\(\Rightarrow\) \(\text{[42n+9-42n-8] ⋮ d}\)
\(\Rightarrow\) \(\text{1 ⋮ d}\)
\(\Rightarrow\) \(\text{d =1( đpcm )}\)
Đúng 3
Bình luận (0)
Chứng minh phân số 12n+5/18n+7 là phân số tối giản với mọi n thuộc z
Gọi (12n + 5;18n + 7) = d
=> \(\hept{\begin{cases}12n+5⋮d\\18n+7⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(12n+5\right)⋮d\\2\left(18n+7\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}36n+15⋮d\\36n+14⋮d\end{cases}}}\)
=> 36n + 15n - (36n + 14) \(⋮\)d
=> 1 \(⋮\)d
=> d \(\in\)Ư(1)
Vì \(n\inℤ\Rightarrow\hept{\begin{cases}12n+5\inℤ\\18n+7\inℤ\end{cases}\Rightarrow d\inℤ}\)
Khi đó d \(\in\left\{1;-1\right\}\)
=> 12n + 5 ; 18n + 7 là 2 số nguyên tố cùng nhau
=> \(\frac{12n+5}{18n+7}\)là phân số tối giản
chứng minh phân số 21n+2/12n+1 là phân số tối giản với mọi số tự nhiên n
chứng minh rằng với mọi số tự nhiên n phân số 21n+4/14n+3 là phân số tối giản
gọi d là ƯCLN của 21n+4 và 14n+3
=> 21n+4 chia hết cho d =>2.(21n+4) chia hết cho d
14n+3 chia hết cho d =>3.(14n+3) chia hết cho d
=> (42n+9)-(42n+8) chia hết cho d
=> 42n+9-42n-8 chia hết cho d
=>1 chia hết cho d
=> d thuộc Ư(1)={1}
=> ƯCLN(21n+4;14n+3)=1 => phân số 21n+4/14n+3 là phân số tối giản (ĐPCM)
Đúng 3
Bình luận (0)
Xem thêm câu trả lời