Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:

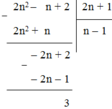
2n2 – n + 2 chia hết cho 2n + 1

⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)

⇔ 2n + 1 ∈ {±1; ±3}

   + 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0

   + 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1

   + 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1

   + 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.

Vậy n ∈ {-2; -1; 0; 1.}

Cách 2:

Ta có:

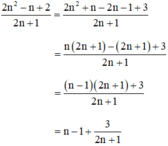
2n2 – n + 2 chia hết cho 2n + 1

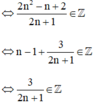
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.

   + 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0

   + 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1

   + 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1

   + 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.

Vậy n ∈ {-2; -1; 0; 1.}

Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.

Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:

2n² – n + 2 chia hết cho 2n + 1

<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)

<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }

   + 2n + 1 = 1 <=> 2n = 0 <=> n = 0

   + 2n + 1 = -1 <=> 2n = -2 <=> n = -1

   + 2n + 1 = 3 <=> 2n = 2 <=> n = 1

   + 2n + 1 = -3 <=> 2n = -4 <=> n = -2.

Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }

\(\frac{2n+4}{n+1}\)   

\(=\frac{2n+2+2}{n+1}\)   

\(=\frac{2n+2}{n+1}+\frac{2}{n+1}\)    

\(=2+\frac{2}{n+1}\)   

Để 2n + 4 chia hết cho n + 1 thì 2 chia hết cho n + 1 

\(\Rightarrow n+1\inƯ\left(2\right)=\left\{1;2\right\}\)   

n + 1 = 1 

n = 0 ( nhận ) 

n + 1 = 2 

n = 1 ( nhận ) 

Vậy n = 0 hoặc n = 1 

(2n+4) \(⋮\) n+1

Ta có : 2n+4 = 2(n+1)+2 

Mà 2(n+1) \(⋮\) n+1 để (2n+4) \(⋮\) n+1 

Thì => 2 \(⋮\) n+1 hay n+1 \(\in\) Ư(2)={1;2}

Ta có bảng sau 

Vậy n\(\in\) {0;1}

2n+4=2n+1+3\([\)2(n+1)\(⋮\)(n+1)\(]\)

Vì 2n+4 chia hết cho n+1 

nên ta có n+1 là ước của 3 hay

  Ư(3)=(1;3)

+)Với n+1=1\(\Rightarrow\)n=0

+) Với n+1=3 \(\Rightarrow\)n=2

- Vậy với n=0;n=2 thì ta có (2n+4)chia hết cho n+1

Bài 1:

\(=-5^{22}+222+[-122-(100-5^{22})+2022]\)

\(=-5^{22}+222-122-100+5^{22}+2022\\ =(-5^{22}+5^{22})+(222-122-100)+2022\\ =0+0+2022=2022\)

Bài 2:

$2n^2+n-6\vdots 2n+1$

$\Rightarrow n(2n+1)-6\vdots 2n+1$

$\Rightarrow 6\vdots 2n+1$

$\Rightarrow 2n+1\in Ư(6)$

Mà $2n+1$ lẻ nên $2n+1\in \left\{\pm 1; \pm 3\right\}$

$\Rightarrow n\in \left\{0; -1; 1; -2\right\}$

a=73

N=40+4

N=20+2

Ko bt

a,ta có :n+4chia hết n+3

          n+3+1 chia hết n+3

          mà n+3 chia hết n+3

suy ra 1 chia hết n+3

n+3 thuộc{1,-1}

n+3=1                                  n+3= -1

n    =1-3                               n    = -1 -3

n     = -2(loại )                     n     = -4

vậy n thuộc tập rỗng

Bạn đăng từng bài 1 thui chứ nếu bạn đăng nhìu như thế này thì khó có ai có thể trả lời hết được bạn ạ

Nhanh lên jùm mình cái , thứ 2 fải nộp bài rùi

a) n + 2 chia hết cho n - 1

    n - 1 + 3 chia hết cho n - 1

        3 chia hết cho n -1

=> n - 1 thuộc Ư(3) = { 1 ;3 }

=> n thuộc { 2;4 }

b) n + 4 chia hết cho n - 2

    n - 2 + 6 chia hết cho n - 2

     6 chia hết cho n - 2

=> n - 2 thuộc Ư(6) = { 1 ; 2 ; 3; 6 }

=> n thuộc { 3 ; 4 ; 5 ; 8 }

c) 2n + 7 chia hết cho n + 1

    2n + 2 + 5 chia hết cho n + 1

   2( n + 1 ) + 5 chia hết cho n + 1

     5 chia hết cho n + 1

=> n + 1 thuộc Ư(5) = { 1; 5 }

=> n thuộc { 0 ; 4 }