xin lỗi bạn nha mik mới học lớp 5 nên không giải đc đâu bạn ơi

Ta có tam giác EDA vuông tại A (phân giác trong và ngoài vuông góc với nhau) 

Từ B vẽ đường vuông góc BC cắt AD tại M (AD phân giác trong của góc A) --> góc ABM = góc B - 90 độ --> góc ABM = góc C .

 dụng góc ngoài của tg ADC --> góc MDB = góc C + góc MAC 

áp dụng góc ngoài tam giác AMB

=> góc BMD = góc MAB + ABM mà góc MAB = MAC (phân giác góc A) và góc ABM = C --> góc BMD = góc MDB --> tg MDB

vuông cân --> góc MDB = 45 độ --> tg EAD vuông cân

t i c k nhé!!!! 6767897854653164457575675676768797897897845665765

Ta có tam giác EDA vuông tại A (phân giác trong và ngoài vuông góc với nhau) 

Từ B vẽ đường vuông góc BC cắt AD tại M (AD phân giác trong của góc A) --> góc ABM = góc B - 90 độ --> góc ABM = góc C .

 dụng góc ngoài của tg ADC --> góc MDB = góc C + góc MAC 

áp dụng góc ngoài tam giác AMB

=> góc BMD = góc MAB + ABM mà góc MAB = MAC (phân giác góc A) và góc ABM = C --> góc BMD = góc MDB --> tg MDB

vuông cân --> góc MDB = 45 độ --> tg EAD vuông cân

Chúc bạn học tốt

Ta có tg EDA vuông tại A (phân giác trong và ngoài vuông góc với nhau) 
Từ B vẽ đường vuông góc BC cắt AD tại M (AD phân giác trong của góc A) --> góc ABM = góc B - 90 độ --> góc ABM = góc C . Áo dụng góc ngoài của tg ADC --> góc MDB = góc C + góc MAC 
áp dung góc ngoài tg AMB --> góc BMD = góc MAB + ABM mà góc MAB = MAC (phân giác góc A) và góc ABM = C --> góc BMD = góc MDB --> tg MDB vuông cân --> góc MDB = 45 độ

--> tg EAD vuông cân

bạn ơi vẽ hình r mình k 2 lần luôn đc ko

vẽ hình kiểu gì thế

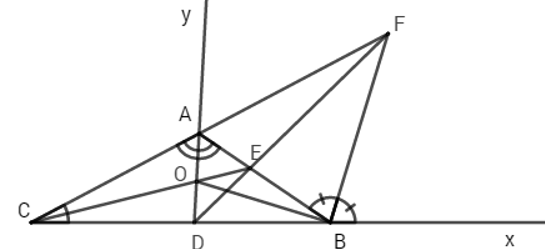
a) Xét   \(\Delta ABC\) có tia phân giác \(BAC,ACB\)  cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\)   (tính chất 3 đường phân giác của tam giác)

\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )

Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)

( tính chất của tia phân giác ) 

Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)

Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)

b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)

\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\)  ( dấu hiệu nhận biết tia phân  giác )

\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )

\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )

Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )

c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng